ЬтФПФкШн
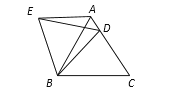
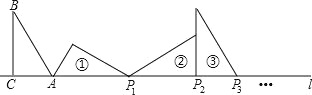
ЁОЬтФПЁПШчЭМRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯBЃН30ЁуЃЌACЃН1ЃЌЧвACдкжБЯпlЩЯЃЌНЋЁїABCШЦЕуAЫГЪБеыа§зЊЕНЂйЃЌПЩЕУЕНЕуP1ЃЌДЫЪБAP1ЃН2ЃЛНЋЮЛжУЂйЕФШ§НЧаЮШЦЕуP1ЫГЪБеыа§зЊЕНЮЛжУЂкЃЌПЩЕУЕНЕуP2ЃЌДЫЪБAP2ЃН2+![]() ЃЛНЋЮЛжУЂкЕФШ§НЧаЮШЦЕуP2ЫГЪБеыа§зЊЕНЮЛжУЂлЃЌПЩЕУЕНЕуP3ЃЌДЫЪБAP3ЃН3+
ЃЛНЋЮЛжУЂкЕФШ§НЧаЮШЦЕуP2ЫГЪБеыа§зЊЕНЮЛжУЂлЃЌПЩЕУЕНЕуP3ЃЌДЫЪБAP3ЃН3+![]() ЃЛЁАДДЫЙцТЩМЬаја§зЊЃЌжБЕНЕуP2020ЮЊжЙЃЌдђAP2020ЕШгк_______ЃЎ
ЃЛЁАДДЫЙцТЩМЬаја§зЊЃЌжБЕНЕуP2020ЮЊжЙЃЌдђAP2020ЕШгк_______ЃЎ
ЁОД№АИЁП![]()
ЁОНтЮіЁП
ИљОнЬтвтЃЌЗЂЯжНЋRtЁїABCШЦЕуAЫГЪБеыа§зЊЃЌУПа§зЊвЛДЮЃЌAPЕФГЄЖШвРДЮдіМг2ЃЌ![]() ЃЌ1ЃЌЧвШ§ДЮвЛбЛЗЃЌАДДЫЙцТЩМДПЩЧѓНтЃЎ
ЃЌ1ЃЌЧвШ§ДЮвЛбЛЗЃЌАДДЫЙцТЩМДПЩЧѓНтЃЎ
НтЃКЁпЁЯACBЃН90ЁуЃЌЁЯBЃН30ЁуЃЌACЃН1ЃЌ
ЁрABЃН2ЃЌBCЃН![]() ЃЌ
ЃЌ
ЁрНЋRtЁїABCШЦЕуAЫГЪБеыа§зЊЃЌУПа§зЊвЛДЮЃЌAPЕФГЄЖШвРДЮдіМг2ЃЌ![]() ЃЌ1ЃЌЧвШ§ДЮвЛбЛЗЃЌ
ЃЌ1ЃЌЧвШ§ДЮвЛбЛЗЃЌ
Ёп2020ЁТ3ЃН673Ё1ЃЌ
ЁрAP2020ЃН673ЃЈ2ЃЋ![]() ЃЋ1ЃЉЃЋ2ЃН2021ЃЋ673
ЃЋ1ЃЉЃЋ2ЃН2021ЃЋ673![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК2021ЃЋ673![]() .
.

СЗЯАВсЯЕСаД№АИ
 вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
ЯрЙиЬтФП