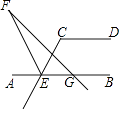题目内容
【题目】如图,AD 是一段斜坡,AB 是水平线,现为了测斜坡上一点 D 的铅直高度(即 垂线段 DB 的长度),小亮在点 D 处立上一竹竿 CD,并保证 CD=AB,CD⊥AD,然后在竿顶 C 处垂下一根细绳(细绳末端挂一重锤,以使细绳与水平线垂直),细绳与斜坡 AD 交于点E,此时他测得 CE=8 m,AE=6 m,求 BD 的长度.

【答案】见解析
【解析】
延长CE交AB于F,根据等角的余角相等求出∠A=∠C,再利用“角角边”证明△ABD和△CDE全等,根据全等三角形对应边相等可得DB=DE.
延长 CE 交 AB 于点 F.
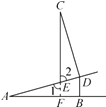
∵∠A+∠1=90°,∠C+∠2=90°,∠1=∠2,
∴∠A=∠C.
在△ABD 和△CDE 中,

∴△ABD≌△CDE(AAS).
∴AD=CE=8 m.
∴BD=DE=AD-AE=2 m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?