题目内容
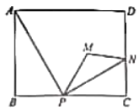
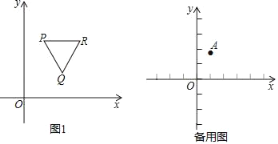
【题目】在平面直角坐标系XOY中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,若P、Q为某等边三角形的两个顶点,且有一边与x轴平行(含重合),则称P、Q互为“向善点”.如图1为点P、Q互为“向善点”的示意图.已知点A的坐标为(1,![]() ),点B的坐标为(m,0)
),点B的坐标为(m,0)
(1)在点M(﹣1,0)、S(2,0)、T(3,3![]() )中,与A点互为“向善点”的是_____;
)中,与A点互为“向善点”的是_____;
(2)若A、B互为“向善点”,求直线AB的解析式;
(3)⊙B的半径为![]() ,若⊙B上有三个点与点A互为“向善点”,请直接写出m的取值范围.
,若⊙B上有三个点与点A互为“向善点”,请直接写出m的取值范围.
【答案】(1)S,T.(2)直线AB的解析式为y=![]() x或y=﹣
x或y=﹣![]() x+2
x+2![]() ;(3)当﹣2<m<0或2<m<4时,⊙B上有三个点与点A互为“向善点”.
;(3)当﹣2<m<0或2<m<4时,⊙B上有三个点与点A互为“向善点”.
【解析】
(1)根据等边三角形的性质结合“向善点”的定义,可得出点S,T与A点互为“向善点”;
(2)根据等边三角形的性质结合“向善点”的定义,可得出关于m的分式方程,解之经检验后可得出点B的坐标,根据点A,B的坐标,利用待定系数法即可求出直线AB的解析式;
(3)分⊙B与直线y=![]() x相切及⊙B与直线y=-
x相切及⊙B与直线y=-![]() x+2
x+2![]() 相切两种情况求出m的值,再利用数形结合即可得出结论.
相切两种情况求出m的值,再利用数形结合即可得出结论.
(1)∵![]() ,
,![]() ,
,
∴点S,T与A点互为“向善点”.
故答案为S,T.
(2)根据题意得:![]() ,
,
解得:m1=0,m2=2,
经检验,m1=0,m2=2均为所列分式方程的解,且符合题意,
∴点B的坐标为(0,0)或(2,0).
设直线AB的解析式为y=kx+b(k≠0),
将A(1,![]() ),B(0,0)或(2,0)代入y=kx+b,得:
),B(0,0)或(2,0)代入y=kx+b,得:
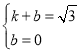 或
或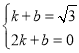 ,
,
解得: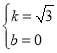 或
或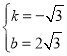 ,
,
∴直线AB的解析式为y=![]() x或y=﹣
x或y=﹣![]() x+2
x+2![]() .
.
(3)当⊙B与直线y=![]() x相切时,过点B作BE⊥直线y=
x相切时,过点B作BE⊥直线y=![]() x于点E,如图2所示.
x于点E,如图2所示.
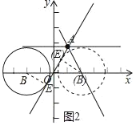
∵∠BOE=60°,
∴sin60°=![]() ,
,
∴OB=2,
∴m=﹣2或m=2;
当⊙B与直线y=﹣![]() x+2
x+2![]() 相切时,过点B作BF⊥直线y=﹣
相切时,过点B作BF⊥直线y=﹣![]() x+2
x+2![]() 于点F,如图3所示.
于点F,如图3所示.
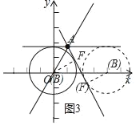
同理,可求出m=0或m=4.
综上所述:当﹣2<m<0或2<m<4时,⊙B上有三个点与点A互为“向善点”.

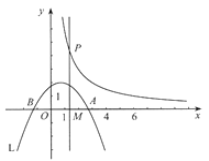
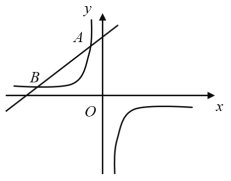
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象相交于
)的图象相交于![]() ,
,![]() 两点.
两点.
(1)求反比例函数的表达式;
(2)将一次函数![]() 的图象沿
的图象沿![]() 轴向下平移
轴向下平移![]() 个单位
个单位![]() ,使平移后的图象与反比例函数
,使平移后的图象与反比例函数![]() 的图象有且只有一个交点,求
的图象有且只有一个交点,求![]() 的值.
的值.
【题目】在春季运动会上,某学校教工组和学生组进行定点投篮比赛,每组均派五名选手参加,每名选手投篮十次,投中记1分,不中记零分,3分以上(含3分)视为合格,比赛成绩绘制成条形统计图如下:
投篮成绩条形统计图
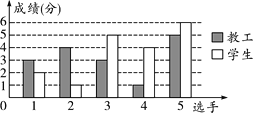
(1)请你根据条形统计图中的数据填写表格:
组别 | 平均数 | 中位数 | 方差 | 合格率 |
教工组 | ________ | 3 | ________ | 80% |
学生组 | 3.6 | ________ | 3.44 | 60% |
(2)如果小亮认为教工组的成绩优于学生组,你认为他的理由是什么?小明认为学生组成绩优于教工组,他的理由又是什么?
(3)若再让一名体育教师投篮后,六名教师成绩平均数大于学生组成绩的中位数,设这名体育教师命中m分,求m的值.