题目内容
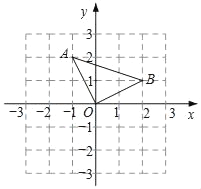
【题目】如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).
(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)
(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为 ,PA+PB的最小值为 .
【答案】(1)作图见解析,A1(1,2),B1(﹣2,1);(2)点P的坐标P(1,0),PA+PB的最小值为![]()
【解析】
(1)分别作出点A和点B关于y轴的对称点,再与点O首尾顺次连接即可;
(2)作点B关于x轴的对称点B′,连接AB′,与x轴的交点即为所求点P,AB′的长即为PA+PB的最小值,利用勾股定理计算可得答案.
(1)如图所示,△A1OB1即为所求;
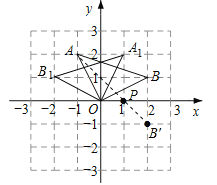
由图知:A1(1,2),B1(﹣2,1);
(2)由图知,点P即为所求,点P的坐标P(1,0),PA+PB的最小值为![]() .
.
故答案为:(1,0),3![]() .
.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案【题目】温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
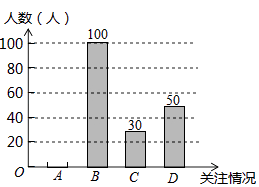
(1)根据上述统计表可得此次采访的人数为人;m= , n=;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,估计25000名温州市民中高度关注瓯江口新区的市民约人.
【题目】爱动脑筋的小明同学在买一双新的运动鞋时,发现了一个有趣现象:即鞋子的码数y(码)与鞋子的长x(cm)之间存在着某种联系.经过收集数据,得到如表:
鞋长x(cm) | … | 22 | 23 | 24 | 25 | 26 | … |
码数y(码) | … | 34 | 36 | 38 | 40 | 42 | … |
请你替小明解决下列问题:
(1)当鞋长为28cm时,鞋子的码数是多少?
(2)写出y与x之间的关系式;
(3)已知姚明的鞋子穿52码时,则他穿的鞋长是多长?