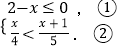题目内容
【题目】有一块形状为四边形的钢板,量得它的各边长度为AB=9cm,BC=12cm,CD=17cm,DA=8cm,∠B=90°.求这块钢板的面积. 
【答案】解:连接AC,在RT△ABC中,AC= ![]() =15,在△ADC中,AD=8cm,CD=17cm,
=15,在△ADC中,AD=8cm,CD=17cm,
则AC2+AD2=DC2 ,
故可得△ADC为直角三角形,
这块钢板的面积=S△ABC+S△ADC= ![]() AB×BC+
AB×BC+ ![]() AD×AC=54+60=114
AD×AC=54+60=114
【解析】连接AC,在RT△ABC中,利用可勾股定理可得出AC,利用勾股定理的逆定理可判断△ADC是直角三角形,分别求出两个直角三角形的面积相加即可.
【考点精析】通过灵活运用勾股定理的概念和勾股定理的逆定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.

练习册系列答案
相关题目
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?