题目内容
【题目】解下列不等式或等式组:
(1)10﹣3(x+5)≤1
(2)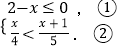 .
.
【答案】
(1)解:10﹣3(x+5)≤1
去括号,得
10﹣3x﹣15≤1,
移项及合并同类项,得
﹣3x≤6
系数化为1,得
x≥﹣2
故原不等式的解集是x≥﹣2;
(2)解: 
由①,得x≥2,
由②,得x<4,
故原不等式组的解集是2≤x<4
【解析】(1)按照去括号、移项、合并同类项、系数化为1的步骤求解即可;
(2)先求得两个方程组的解集,然后再依据同大取大、同小取小,大小小大中间找,大大小小找不着确定出不等式组的解集即可.
【考点精析】根据题目的已知条件,利用一元一次不等式的解法和一元一次不等式组的解法的相关知识可以得到问题的答案,需要掌握步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题);解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).

练习册系列答案
相关题目
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.