Question

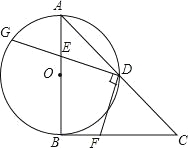
【题目】(2016山东潍坊第21题)正方形ABCD内接于⊙O，如图所示，在劣弧上取一点E，连接DE、BE，过点D作DF∥BE交⊙O于点F，连接BF、AF，且AF与DE相交于点G，求证：

（1）四边形EBFD是矩形；

（2）DG=BE．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

试题分析：（1）根据正方形的性质、圆周角定理及平行线的性质易证∠BED=∠BAD=90°，∠BFD=∠BCD=90°，∠EDF=90°，即可判定四边形EBFD是矩形；（2）根据正方形的性质可得弧AD的度数是90°，进而得出BE=DF，则BE=DG．

试题解析：（1）∵正方形ABCD内接于⊙O，

∴∠BED=∠BAD=90°，∠BFD=∠BCD=90°，

又∵DF∥BE，

∴∠EDF+∠BED=180°，

∴∠EDF=90°，

∴四边形EBFD是矩形；

（2））∵正方形ABCD内接于⊙O，

∴弧AD的度数是90°，

∴∠AFD=45°，

又∵∠GDF=90°，

∴∠DGF=∠DFC=45°，

∴DG=DF，

又∵在矩形EBFD中，BE=DF，

∴BE=DG．