题目内容
【题目】若三个非零实数![]() 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数
满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数![]() 构成“和谐三数组”.
构成“和谐三数组”.
(1)实数1,2,3可以构成“和谐三数组”吗?请说明理由.
(2)若![]() 三点均在函数y=
三点均在函数y=![]() (
(![]() 为常数,
为常数,![]() )的图象上,且这三点的纵坐标
)的图象上,且这三点的纵坐标![]() 构成“和谐三数组”,求实数
构成“和谐三数组”,求实数![]() 的值;
的值;
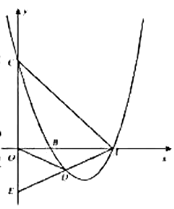
(3)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点.
两点.
①求证:A,B,C三点的横坐标x1,x2,x3构成“和谐三组数”;
②若a>2b>3c,x2=1,求点P(,)与原点O的距离OP的取值范围.
【答案】(1)不可以(2)t=-4,-2或2(3)![]() 且OP≠1
且OP≠1
【解析】
试题分析:(1)根据“和谐三组数”的意义直接判断即可;
(2)分别表示出M、N、R的坐标,然后根据“和谐三组数”求出t的值;
(3)①令y=2bx+2c=0表示出x1,然后联立方程组得到![]() ,然后由韦达定理表示出x2、x3的关系,从而判断;
,然后由韦达定理表示出x2、x3的关系,从而判断;
②由已知求出OP表达式,然后根据表达式求范围.
试题解析:(1)由已知1<2<3
∴![]()
又∵1≠![]()
∴1,2,3不可以构成“和谐三组数”
(2)M(t,![]() ),N(t+1,
),N(t+1,![]() ),R(t+3,
),R(t+3,![]() )
)
![]() ,
,![]() ,
,![]() 组成“和谐三组数”
组成“和谐三组数”
①若![]() =
=![]() +
+![]() ,得t=-4
,得t=-4
②若![]() ,得t=-2
,得t=-2
③若![]() ,得t=2
,得t=2
综上,t=-4,-2或2
(3)①令y=2bx+2c=0
∴x1=-![]()
联立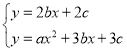
∴![]()
∴由韦达定理可得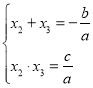
∴![]()
∴![]() 构成“和谐三组数”
构成“和谐三组数”
②∵x2=1
∴a+b+c=0
∴c=-a-b
∴OP=![]() =
=![]()
∵a>2b>3c
∴-![]() <b<
<b<![]()
∴-![]() <
<![]() <
<![]()
令t=![]() ,p=2
,p=2![]() =
=![]()
∵-![]() <t<
<t<![]() 且t≠-1或0
且t≠-1或0
∴![]() <p<
<p<![]() 且p≠1
且p≠1
∴![]() 且OP≠1
且OP≠1

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目