题目内容
如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度,当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
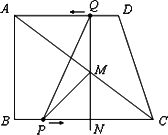
(1)NC=________;MC=________.(用含t的代数式表示);
(2)当t为何值时,四边形PCDQ构成平行四边形?
(3)是否存在某一时刻t,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;
(4)探究:t为何值时,△PMC为等腰三角形?
解析:
|
解:(1)NC=1+t,MC= (2)∵QD∥PC,∴当QD=PC时,四边形PCDQ构成平行四边形 ∴t=4-t,∴t=2 ∴当t=2时,四边形PCDQ构成平行四边形;3分 (3)若射线QN将△ABC的周长平分,则有MC+NC=AM+BN+AB ∴ 解得t= ∵MN= ∴S△MNC= 当t= ∵ ∴不存在某一时刻t,使射线QN恰好将△ABC的面积和周长同时平分 (4)若△PMC为等腰三角形,则: ①当MP=MC时(如图1),则有:NP=NC
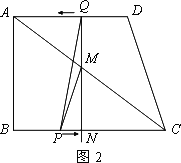
即PC=2NC,∴4-t=2(1+t)解得t= ②当CM=CP时(如图2),则有:
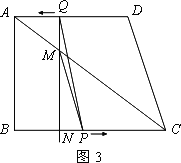
③当PM=PC时(如图3),则有:
在Rt△MNP中,PM2=MN2+PN2又MN= PN=NC-PC=(1+t)-(4-t)=2t-3 ∴[ (或过P作PE⊥AC于E,用△CPE∽△CAB得 综上所述,当t= |

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
 如图,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED.
如图,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED. 21、当我们遇到梯形问题时,我们常用分割的方法,将其转化成我们熟悉的图形来解决:
21、当我们遇到梯形问题时,我们常用分割的方法,将其转化成我们熟悉的图形来解决:
 如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )
如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( ) 如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD的中点,点F是AB上的点,∠ADF=45°,FE=a,梯形ABCD的面积为m.
如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD的中点,点F是AB上的点,∠ADF=45°,FE=a,梯形ABCD的面积为m. 如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为y cm2.
如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为y cm2.