题目内容
设计一个商标图形（如图所示），在△ABC中，AB=AC=2cm，∠B=30°，以A为圆心，AB为半径作 |
| BEC |
|
| BFC |
分析：由图可知：商标图案的面积=半圆CBF的面积+△ABC的面积-扇形ABC的面积，可根据各自的面积计算方法求出商标图案的面积．
解答：解：S扇形ACB=
=
，S半圆CBF=
π×（
）2=
，S△ABC=
×2
×1=
；
所以商标图案面积=S半圆CBF+S△ABC-S扇形ACB=
+
-
=（
+
）cm2．
| 120π×4 |
| 360 |
| 4π |
| 3 |
| 1 |
| 2 |
| 3 |
| 3π |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
所以商标图案面积=S半圆CBF+S△ABC-S扇形ACB=
| 3π |
| 2 |
| 3 |
| 4π |
| 3 |
| π |
| 6 |
| 3 |
点评：本题主要考查了扇形和三角形的面积计算方法．不规则图形的面积通常转化为规则图形的面积的和差．
练习册系列答案
阅读快车系列答案
相关题目
24、如图是一个由12个相似（形状相同，大小不同）的直角三角形所组成的图案，它是否有点像一个商标图案？你能否也用相似图形设计出几个美丽的图案？最好再给你设计的图案取一个名字．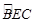
,以BC为直径作半圆BFC,则商标图案面积等于________cm2.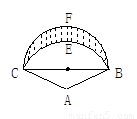
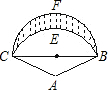设计一个商标图形（如图所示），在△ABC中，AB=AC=2cm，∠B=30°，以A为圆心，AB为半径作
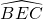，以BC为直径作半圆
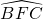，则商标图案面积等于________cm2．
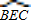，以BC为直径作半圆
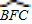，则商标图案面积等于 cm2．