题目内容
如图，有一个直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿∠CAB的角平分线AD折叠，使它落在斜边AB上，且与AE重合，你能求出CD的长吗？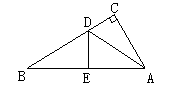
3cm
本题考查了折叠的性质，勾股定理的应用
由折叠的性质可知DE=CD，AC=AE，∠AED=∠C=90°，在Rt△ABC中，由勾股定理求AB，由BE=AB-AE，设CD=DE=x，则BD=8-x，在Rt△BDE中，由勾股定理求x即可．
能，
∵△ABC为直角三角形，且AC=6cm，BC=8cm，
由勾股定理得；AB=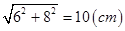
又∵△ADE是△ADC翻折所得；
∴DC=DE，AC=AE=6cm，BE=10-6=4cm，
设DC=x，则BD=8-x
在Rt△BDE中，由勾股定理：
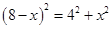
解得x=3
∴DC的长为3cm.
由折叠的性质可知DE=CD，AC=AE，∠AED=∠C=90°，在Rt△ABC中，由勾股定理求AB，由BE=AB-AE，设CD=DE=x，则BD=8-x，在Rt△BDE中，由勾股定理求x即可．
能，
∵△ABC为直角三角形，且AC=6cm，BC=8cm，
由勾股定理得；AB=
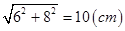
又∵△ADE是△ADC翻折所得；
∴DC=DE，AC=AE=6cm，BE=10-6=4cm，
设DC=x，则BD=8-x
在Rt△BDE中，由勾股定理：
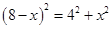
解得x=3
∴DC的长为3cm.
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
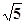的对应的点。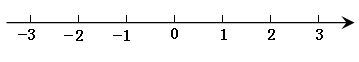
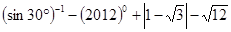
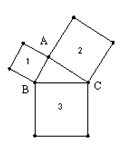
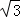，则这个矩形的两条对角线所成的锐角是_________．
中，若
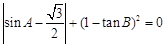，则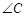
的度数是（ ）
