Question

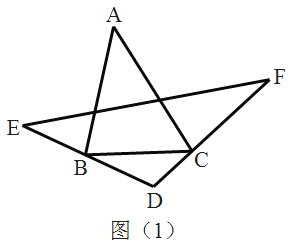
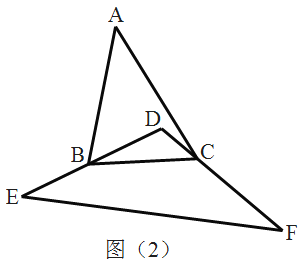
【题目】如图，∠BAD=∠CAE=90o，AB=AD，AE=AC.

（1）若AC=10，求四边形ABCD的面积；

（2）求证：AC平分∠ECF；

Answer 1

【答案】（1）50（2）见解析

【解析】

（1）求出∠BAC＝∠EAD，根据SAS推出△ABC≌△ADE，推出四边形ABCD的面积＝三角形ACE的面积，即可得出答案；

（2）根据等腰直角三角形的性质得出∠ACE＝∠AEC＝45°，△ABC≌△ADE求出∠ACB＝∠AEC＝45°，推出∠ACB＝∠ACE即可；

（1）∵∠BAD＝∠CAE＝90°，

∴∠BAC＋∠CAD＝∠EAD＋∠CAD

∴∠BAC＝∠EAD，

在△ABC和△ADE中，

，

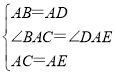∴△ABC≌△ADE（SAS），

∵S四边形ABCD＝S△ABC＋S△ACD，

∴S四边形ABCD＝S△ADE＋S△ACD＝S△ACE＝×102＝50；

（2）证明：∵△ACE是等腰直角三角形，

∴∠ACE＝∠AEC＝45°，

由△ABC≌△ADE得：

∠ACB＝∠AEC＝45°，

∴∠ACB＝∠ACE，

∴AC平分∠ECF.