题目内容
【题目】AD是△ABC的边BC上的中线，AB=6，AC=4，则边BC的取值范围是 ， 中线AD的取值范围是 ．
【答案】2＜BC＜10；1＜AD＜5
【解析】解：∵在△ABC中，AB=6，AC=4， ∴6﹣4＜BC＜6+4，
∴2＜BC＜10；
延长AD到E，使AD=DE，连接BE，如图所示：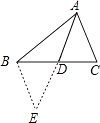
∵AD为中线，
∴BD=DC，
在△ADC和△EDB中， 
，
∴△ADC≌△EDB（SAS），
∴AC=BE=4，
在△ABE中，AB=6，BE=4，
∴6﹣4＜AE＜6+4，
∴2＜2AD＜10，
∴1＜AD＜5，
故答案为：2＜BC＜10，1＜AD＜5．
根据三角形的三边关系定理求出BC的范围即可；延长AD到E，使AD=DE，连接BE，证三角形全等，推出BE=AC=6，在三角形ABE中，根据三角形的三边关系定理求出即可．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
