题目内容
【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.
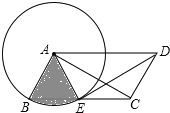
(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
【答案】(1)见解析;(2)![]() π.
π.
【解析】
试题分析:(1)由四边形ABCD是平行四边形,AB=AE,易证得四边形AECD是等腰梯形,即可得AC=DE,然后由SSS,即可证得:△AED≌△DCA;
(2)由DE平分∠ADC且与⊙A相切于点E,可求得∠EAD的度数,继而求得∠BAE的度数,然后由扇形的面积公式求得阴影部分(扇形)的面积.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴四边形AECD是梯形,
∵AB=AE,
∴AE=CD,
∴四边形AECD是等腰梯形,
∴AC=DE,
在△AED和△DCA中,
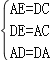 ,
,
∴△AED≌△DCA(SSS);
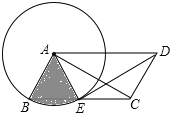
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵四边形AECD是等腰梯形,
∴∠DAE=∠ADC=2∠ADE,
∵DE与⊙A相切于点E,
∴AE⊥DE,
即∠AED=90°,
∴∠ADE=30°,
∴∠DAE=60°,
∴∠DCE=∠AEC=180°﹣∠DAE=120°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠DCE=120°,
∴∠BAE=∠BAD﹣∠EAD=60°,
∴S阴影=![]() ×π×22=
×π×22=![]() π.
π.

练习册系列答案
相关题目