Question

若x₁，x₂是关于x的方程x²+bx+c=0的两个实数根，且|x₁|+|x₂|=2|k|（k是整数），则称方程x²+bx+c=0为“偶系二次方程”．如方程x²﹣6x﹣27=0，x²﹣2x﹣8=0，，x²+6x﹣27=0，x²+4x+4=0，都是“偶系二次方程”．

（1）判断方程x²+x﹣12=0是否是“偶系二次方程”，并说明理由；

（2）对于任意一个整数b，是否存在实数c，使得关于x的方程x²+bx+c=0是“偶系二次方程”，并说明理由．

 

Answer 1

【答案】

（1）不是。理由见解析

（2）存在。理由见解析

【解析】

试题分析：（1）求出原方程的根，再代入|x₁|+|x₂|看结果是否为2的整数倍就可以得出结论。

（2）设c=mb²+n，由条件x²﹣6x﹣27=0和x²+6x﹣27=0是偶系二次方程建模，就可以表示出c，然后根据公式法就可以求出其根，再代入|x₁|+|x₂|就可以得出结论。

解：（1）不是。理由如下：

解方程x²+x﹣12=0得，x₁=3，x₂=﹣4。

|x₁|+|x₂|=3+4=7=2×3.5．

∵3.5不是整数，∴x²+x﹣12=0不是“偶系二次方程。；

（2）存在。理由如下：

假设c=mb²+n，

∵x²﹣6x﹣27=0和x²+6x﹣27=0是偶系二次方程，

∴当b=﹣6，c=﹣27时，﹣27=36m+n。

∵x²=0是偶系二次方程，∴n=0时，m=。∴c=b²。

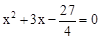∵是偶系二次方程，当b=3时，c=×3²。

∴可设c=b²。

对于任意一个整数b，c=b²时，

△=b²﹣4c=4b²≥0，，∴x₁=b，x₂=b。

∴|x₁|+|x₂|=2b。

∵b是整数，

∴对于任何一个整数b，c=b²时，关于x的方程x²+bx+c=0是“偶系二次方程”。