Question

【题目】如图，在矩形ABCD中，AB=6，AD=4，过矩形ABCD的对角线交点O作直线分别交CD、AB于点E、F，连接AE，若△AEF是等腰三角形，则DE=______．

Answer 1

【答案】或2

【解析】

连接AC，如图1所示：由矩形的性质得到∠D=90°，AD=BC=4，OA=OC，AB∥DC，求得∠OAF=∠OCE，根据全等三角形的性质得到AF=CE，若△AEF是等腰三角形，分三种情讨论：

①当AE=AF时，如图1所示：设AE=AF=CE=x，则DE=6-x，根据勾股定理即可得到结论；

②当AE=EF时，作EG⊥AF于G，如图2所示：设AF=CE=x，则DE=6-x，AG=x，列方程即可得到结论；

③当AF=FE时，作FH⊥CD于H，如图3所示：设AF=FE=CE=x，则BF=6-x，则CH=BF=6-x，根据勾股定理即可得到结论．

解：连接AC，如图1所示：

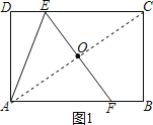
∵四边形ABCD是矩形，

∴∠D=90°，AD=BC=4，OA=OC，AB∥DC，

∴∠OAF=∠OCE，

在△AOF和△COE中，，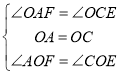

∴△AOF≌△COE（ASA），

∴AF=CE，

若△AEF是等腰三角形，分三种情讨论：

①当AE=AF时，如图1所示：

设AE=AF=CE=x，则DE=6-x，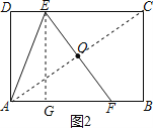

在Rt△ADE中，由勾股定理得：42+（6-x）2=x2，

解得：x=，即DE=；

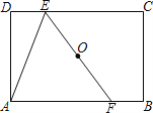
②当AE=EF时，

作EG⊥AF于G，如图2所示：

则AG=AE=DE，

设AF=CE=x，则DE=6-x，AG=x，

∴x=6-x，解得：x=4，

∴DE=2；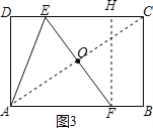

③当AF=FE时，作FH⊥CD于H，如图3所示：

设AF=FE=CE=x，则BF=6-x，则CH=BF=6-x，

∴EH=CE-CH=x-（6-x）=2x-6，

在Rt△EFH中，由勾股定理得：42+（2x-6）2=x2，

整理得：3x2-24x+52=0，

∵△=（-24）2-4×3×52＜0，

∴此方程无解；

综上所述：△AEF是等腰三角形，则DE为或2；

故答案为：或2．