题目内容
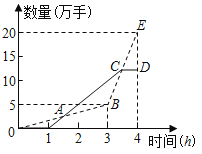
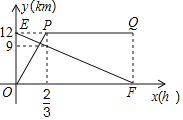
【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x(h)之间的函数关系.
(1)求线段OP对应的y甲与x的函数关系式并注明自变量x的取值范围;
(2)求y乙与x的函数关系式以及乙到达A地所用的时间;
(3)经过 小时,甲、乙两人相距2km.
【答案】(1)y甲=18x(0<x<![]() );(2)y乙=﹣4.5x+12, 乙到达A地所用的时间
);(2)y乙=﹣4.5x+12, 乙到达A地所用的时间![]() 小时;(3)
小时;(3)![]() 或
或![]()
【解析】
(1)根据函数图象中的数据,利用待定系数法可以求得线段OP对应的y甲与x的函数关系式;
(2)利用待定系数法可以求得y乙与x的函数关系式以及乙到达A地所用的时间;
(3)根据(1)和(2)中的函数解析式,可以求得经过多少小时,甲、乙两人相距2km.
(1)设线段OP对应的y甲与x的函数关系式为y甲=kx(k≠0),
12=![]() k,得k=18,
k,得k=18,
即线段OP对应的y甲与x的函数关系式为y甲=18x(0<x<![]() );
);
故答案为:y甲=18x(0<x<![]() )
)
(2)设y乙与x的函数关系式为y乙=ax+b,
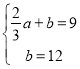 ,
,
解得![]() ,
,
即y乙与x的函数关系式为y乙=﹣4.5x+12,
当y乙=0时,﹣4.5x+12=0,解得x=![]() ,
,
∴乙到达A地所用的时间![]() 小时;
小时;
故答案为:![]() 小时
小时
(3)|(﹣4.5x+12)﹣18x|=2,
﹣4.5x+12﹣18x=2或18x﹣(﹣4.5x+12)=2,
解得,x=![]() 或x=
或x=![]() ,
,
∴经过![]() 或
或![]() 小时,甲、乙两人相距2km.
小时,甲、乙两人相距2km.
故答案为:![]() 或
或![]() .
.

 赢在课堂名师课时计划系列答案
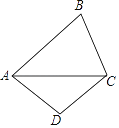
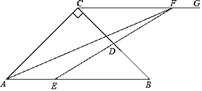
赢在课堂名师课时计划系列答案【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=6cm,E是线段AB上一动点,D是BC的中点,过点C作射线CG,使CG∥AB,连接ED,并延长ED交CG于点F,连接AF.设A,E两点间的距离为xcm,A,F两点间的距离为y1cm,E,F两点间的距离为y2cm.小丽根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小丽的探究过程,请补充完整:
(1)按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 9.49 | 8.54 | 7.62 | 6.71 | 5.83 | 5.00 | 4.24 |
y2/cm | 9.49 | 7.62 | 5.83 | 3.16 | 3.16 | 4.24 |
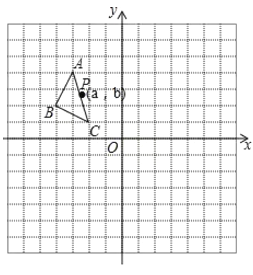
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;

(3)结合函数图象,解决问题:当△AEF为等腰三角形时,AE的长度约为 cm.