题目内容
【题目】如图,抛物线y=―![]() x2+(6―
x2+(6―![]() )x+m―3与x轴交于A(x1,0)、B(x2,0)两点(x1<x2),交y轴于C点,且x1+x2=0。
)x+m―3与x轴交于A(x1,0)、B(x2,0)两点(x1<x2),交y轴于C点,且x1+x2=0。
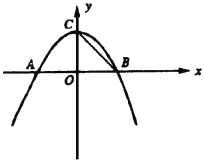
(1)求抛物线的解析式,并写出顶点坐标及对称轴方程。
(2)在抛物线上是否存在一点P使△PBC≌△OBC,若存在,求出点P的坐标,若不存在,请说明理由。
【答案】(1)![]() ,C(0,3),对称轴x=0;(2)不存在,理由详见解析.
,C(0,3),对称轴x=0;(2)不存在,理由详见解析.
【解析】
1)根据![]() ,可得出抛物线的对称轴为y轴即x=0,由此可求出m的值.进而可求出抛物线的解析式.根据抛物线的解析式即可得出其顶点坐标和对称轴方程.△PBC≌△OBC.
,可得出抛物线的对称轴为y轴即x=0,由此可求出m的值.进而可求出抛物线的解析式.根据抛物线的解析式即可得出其顶点坐标和对称轴方程.△PBC≌△OBC.
(2)如果△PBC≌△OBC,由于△OBC是等腰直角三角形,那么P有两种可能:①P,O重合;②P与O关于直线BC对称,而这两种P点均不在抛物线上,因此不存在这样的P点.
:(1) ∵![]()
∴6-![]() =0
=0
∴m=![]() 51
51![]() 抛物线与y轴交于正半轴上,
抛物线与y轴交于正半轴上,
∴m=6.
抛物线解析式![]()
∴抛物线顶点坐标C(3,0),抛物线对称轴方程x=0.
(2)B点坐标为(3,0),
假设存在一点P使△PBC≌△OBC.
因为△OBC是等腰直角三角形,BC是公共边,
故P点与O点必关于BC所在直线对称.点P坐标是(3,3).
当x=3时,y![]() 3,即点P不在抛物线上,
3,即点P不在抛物线上,
所以不存在这样的点P,使△PBC≌△OBC.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目