题目内容
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF. 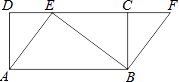
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠BCD=90°.
∴∠BCF=180°﹣∠BCD=180°﹣90°=90°.
∴∠D=∠BCF.在Rt△ADE和Rt△BCF中,
![]()
∴Rt△ADE≌Rt△BCF.
∴∠1=∠F.
∴AE∥BF.
∵AE=BF,
∴四边形ABFE是平行四边形

(2)解:∵∠D=90°,
∴∠DAE+∠1=90°.
∵∠BEF=∠DAE,
∴∠BEF+∠1=90°.
∵∠BEF+∠1+∠AEB=180°,
∴∠AEB=90°.
在Rt△ABE中,AE=3,BE=4,
AB= ![]() .
.
∵四边形ABFE是平行四边形,
∴EF=AB=5
【解析】(1)欲证明四边形ABFE是平行四边形,只要证明AE∥BF,EF∥AB即可.(2)先证明△AEB是直角三角形,再根据勾股定理计算即可.
【考点精析】通过灵活运用平行四边形的判定与性质和矩形的性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目