题目内容
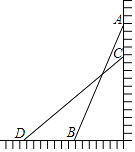
【题目】已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形. 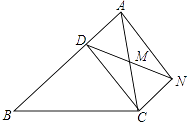
【答案】证明:∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,
∵  ,
,
∴△AMD≌△CMN(ASA),
∴AD=CN.
又∵AD∥CN,
∴四边形ADCN是平行四边形.
又∵∠BAN=90度,
∴四边形ADCN是矩形
【解析】通过证明△AMD≌△CMN得到对应边AD=CN;结合已知条件“CN∥AB”判定四边形ADCN是平行四边形;再根据“有一内角为直角的平行四边形是矩形”证得结论.
【考点精析】本题主要考查了矩形的判定方法的相关知识点,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目