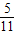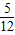题目内容
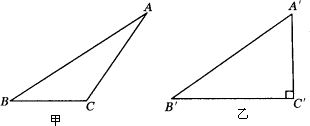
在已知三角形的三边上,分别取其二等分点、三等分点、四等分点、五等分点…,如图所示,连接各分点,依此规律,则第10个图形中,其阴影部分的面积与整个三角形面积的比为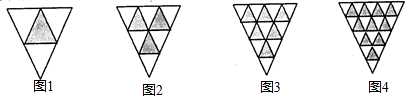
- A.
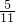
- B.
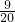
- C.

- D.
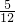
A
分析:先看小三角形总数4,9,16,…,所以第10个图形一共有112=121个小三角形,阴影三角形个数1,1+2,1+2+3,…,所以第10个图形有1+2+3+…+10=55个小三角形,所以即可得出阴影部分面积与整个三角形面积的比.
解答:∵取其二等分点、三等分点、四等分点、五等分点…,
∴每一个小三角形都与原三角形相似,
∵图中小三角形总数4,9,16,…,则第10个图中小三角形共有121个,
阴影三角形个数1,1+2,1+2+3,…,则第10个图形有55个,
∴阴影部分的面积与整个三角形面积的比为55:121=5:11.
故选A.
点评:本题是一道找规律的题目,考查了相似三角形的判定和性质,解题的关键是找出图中的三角形个数的规律.
分析:先看小三角形总数4,9,16,…,所以第10个图形一共有112=121个小三角形,阴影三角形个数1,1+2,1+2+3,…,所以第10个图形有1+2+3+…+10=55个小三角形,所以即可得出阴影部分面积与整个三角形面积的比.
解答:∵取其二等分点、三等分点、四等分点、五等分点…,
∴每一个小三角形都与原三角形相似,
∵图中小三角形总数4,9,16,…,则第10个图中小三角形共有121个,
阴影三角形个数1,1+2,1+2+3,…,则第10个图形有55个,
∴阴影部分的面积与整个三角形面积的比为55:121=5:11.
故选A.
点评:本题是一道找规律的题目,考查了相似三角形的判定和性质,解题的关键是找出图中的三角形个数的规律.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
在已知三角形的三边上,分别取其二等分点、三等分点、四等分点、五等分点…,如图所示,连接各分点,依此规律,则第10个图形中,其阴影部分的面积与整个三角形面积的比为( )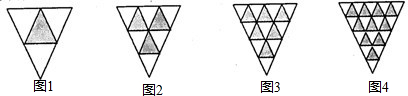

A、
| ||
B、
| ||
C、
| ||
D、
|
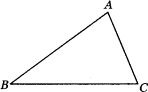
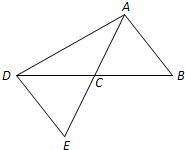 23、如图,A、B两点分别位于一池塘两侧,池塘左边有一水房D,在DB中点C处有一棵百年古槐,小明从A点出发,沿AC一直向前走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量出点E到水房D的距离,则DE的长度就是A、B两点间的距离.
23、如图,A、B两点分别位于一池塘两侧,池塘左边有一水房D,在DB中点C处有一棵百年古槐,小明从A点出发,沿AC一直向前走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量出点E到水房D的距离,则DE的长度就是A、B两点间的距离.