题目内容
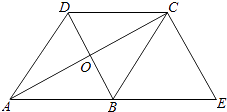
【题目】如图，在菱形ABCD中，对角线AC、BD交于点O，E为AD的中点，菱形ABCD的周长为32，则OE的长等于（ ）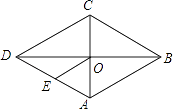 
A.2
B.4
C.8
D.16
【答案】B
【解析】解：∵四边形ABCD是菱形，
∴AC⊥BD，AB=BC=CD=AD，
∴∠AOD=90°，
又∵AB+BC+CD+AD=32．
∴AD=8，
在Rt△AOD中，OE是斜边上的中线，
∴OE= 
AD=4．
故选B．
【考点精析】关于本题考查的三角形中位线定理和菱形的性质，需要了解连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能得出正确答案．
名校课堂系列答案【题目】航模兴趣小组的老师想知道全组学生的年龄情况，于是让大家把自己的年龄写在纸上，下表是全组40名学生的年龄（单位：岁）．
14 | 13 | 13 | 15 | 16 | 12 | 14 | 16 | 17 | 13 |
14 | 15 | 12 | 12 | 13 | 14 | 15 | 16 | 15 | 14 |
13 | 12 | 15 | 14 | 17 | 16 | 16 | 13 | 12 | 14 |
14 | 15 | 13 | 16 | 15 | 16 | 17 | 14 | 14 | 13 |
（1）在这个统计表中，13岁的频数是多少？频率是多少？
（2）多少岁的频率最大，这个最大频率是多少？
（3）假如老师随机地问一名学生的年龄，你认为老师最可能听到的回答是多少岁？
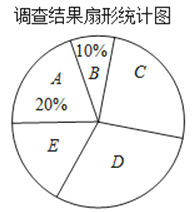
【题目】从2013年1月7日起，中国中东部大部分地区持续出现雾霾天气，某市记者为了了解“雾霾天气的主要成因”，随机调查了该市部分市民，并对调查结果进行整理，绘制了如下尚不完整的统计图表．
组别 | 观点 | 频数（人数） |
A | 大气气压低，空气不流动 | 80 |
B | 地面灰尘大，空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题：
（Ⅰ）求接受调查的总人数；
（Ⅱ）m、n各等于多少？扇形统计图中E组所占的百分比是多少？
（Ⅲ）若该市人口约有100万人，请你估计其中持D组“观点”的市民人数．