题目内容
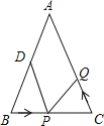
【题目】如图,在△ABC中,AB=AC=5,∠B=∠C,BC=8,点D从B点出发沿线段BC向C运动(D不与B、C重合),点E从点C出发沿线段CA向A运动(E不与A、C重合),它们以相同的速度同时运动,连结AD、DE.若要使△ABD≌△DCE,①请给出确定D、E两点位置的方法(如指明CD长度等),并说明理由;②此时∠ADE与∠C大小关系怎样?为什么?

【答案】①CD=5时,△ABD≌△DCE;②∠ADE=∠C,理由见解析;
【解析】
①CD=5时,根据SAS推出△ABD≌△DCE即可.
②根据全等三角形性质得出∠BDA=∠DEC,根据三角形内角和定理求出∠C=180°-∠ADB-∠EDC,求出∠ADE=180°-∠BDA-∠EDC,即可得出答案.
①DC=5,
理由是:∵BC=8,CD=AB=5,
∴BD=85=3,
即CE=BD=3,
在△ABD和△DCE中,
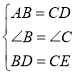 ,
,
∴△ABD≌△DCE,
即当CD=5时,△ABD≌△DCE.
②∠ADE=∠C,
理由是:∵△ABD≌△DCE,
∴∠BDA=∠DEC,
∴∠C=180°∠DEC∠EDC=180°∠ADB∠EDC,
∵∠ADE=180°∠BDA∠EDC,
∴∠ADE=∠C.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目