Question

【题目】二次函数y=- (x-2)2+7，当m≤x≤n且mn＜0时，y的最小值为2m，最大值为2n，则m+n的值为( )

A. 2 B. C. D.

Answer 1

【答案】B

【解析】分析：条件m≤x≤n和mn＜0可得m＜0，n＞0，

所以y的最小值为2m为负数，最大值为2n为正数．

最大值为2n分两种情况，（1）顶点纵坐标取到最大值，求出n=3.5，结合图象最小值只能由x=m时求出．

（2）顶点纵坐标取不到最大值，结合图象最大值只能由x=n求出，最小值只能由x=m求出．

详解：二次函数y=﹣（x﹣2）2+7的大致图象如下：

．

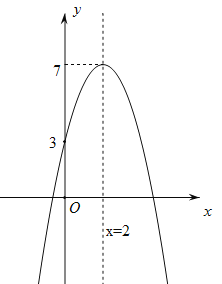①当m≤0≤x≤n＜2时，当x=m时y取最小值，即2m=﹣（m﹣2）2+7，解得：m=－1，或m=3(舍去)．

当x=n时y取最大值，即2n=﹣（n﹣2）2+7，解得：n=－1或n=3(均不符合题意，舍去)；

②当m≤0≤x≤2≤n时，当x=m时y取最小值，即2m=﹣（m﹣2）2+7，解得：m=－1，或m=3(舍去)．

当x=2时y取最大值，即2n=﹣（2﹣2）2+7，解得：n=，

或x=n时y取最小值，x=2时y取最大值，2m=﹣（n﹣2）2+7，n=，∴m=．

∵m＜0，∴此种情形不合题意，

综上所述：m=－1，n=，m+n=﹣1+=．

故选B．