题目内容
已知在等腰△ABC中,∠A=70°,AB=AC,则∠B为
- A.70°
- B.45°
- C.55°
- D.65°
C
分析:首先由AB=AC得到∠B=∠C,再由∠A+∠B+∠C=180°即可求出∠B.
解答: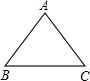 解:∵AB=AC,
解:∵AB=AC,
∴∠B=∠C,
∵∠A+∠B+∠C=180°,∠A=70°
∴∠B= (180°-70°)=55°.
(180°-70°)=55°.
故选C.
点评:本题考查了等腰三角形的性质,三角形的内角和定理等知识点,利用性质进行证明和计算是解此题的关键.
分析:首先由AB=AC得到∠B=∠C,再由∠A+∠B+∠C=180°即可求出∠B.
解答:
 解:∵AB=AC,
解:∵AB=AC,∴∠B=∠C,
∵∠A+∠B+∠C=180°,∠A=70°
∴∠B=
 (180°-70°)=55°.
(180°-70°)=55°.故选C.
点评:本题考查了等腰三角形的性质,三角形的内角和定理等知识点,利用性质进行证明和计算是解此题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知在等腰△ABC中,∠A=70°,AB=AC,则∠B为( )
| A、70° | B、45° | C、55° | D、65° |
 如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
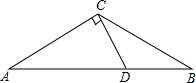
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D. 如图,已知在等腰△ABC中,∠ACB=120°.
如图,已知在等腰△ABC中,∠ACB=120°.