题目内容
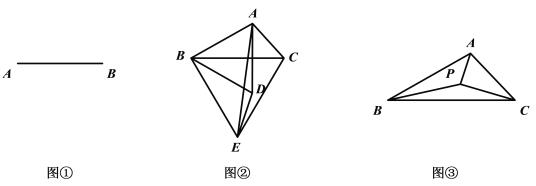
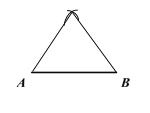
【题目】(1)如图①,已知线段![]() ,以
,以![]() 为一边作等边
为一边作等边![]() (尺规作图,保留作图痕迹,不写作法);
(尺规作图,保留作图痕迹,不写作法);
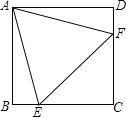
(2)如图②,已知![]() ,
,![]() ,
,![]() ,分别以
,分别以![]() 为边作等边
为边作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,求
,求![]() 的最大值;
的最大值;
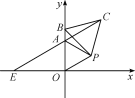
(3)如图③,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() ,求出
,求出![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)5;(3)![]()
【解析】
(1)首先分别以A,B为圆心,以线段AB长为半径为半径画弧,两弧的交点为C ,最后连接AB ,AC就行了;
(2)以点E为中心,将△ACE逆时针旋转60°,则点C落在点B,点A落在点E′.连接AE′,CE′,当点E′、A、C在一条直线上时,AE有最大值.
(3)首先以点B为中心,将△ABP逆时针旋转90°,则点A落在A′,点P落在P′,当A′、P′、P、C在一条直线上时,![]() 取得最小值,然后延长A′B,过点C作CD⊥A′B,利用勾股定理即可得解.
取得最小值,然后延长A′B,过点C作CD⊥A′B,利用勾股定理即可得解.
(1)如图所示:
(2)根据题意,以点E为中心,将△ACE逆时针旋转60°,则点C落在点B,点A落在点E′.连接AE′,CE′,当点E′、A、C在一条直线上时,AE有最大值,如图所示:
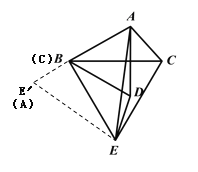
∵E′B=AC,EE′=AE=AE′,![]() ,
,![]() ,
,
∴AE的最大值为3+2=5;
(3)以点B为中心,将△ABP逆时针旋转90°,则点A落在A′,点P落在P′,当A′、P′、P、C在一条直线上时,![]() 取得最小值,延长A′B,过点C作CD⊥A′B于D,如图所示:
取得最小值,延长A′B,过点C作CD⊥A′B于D,如图所示:
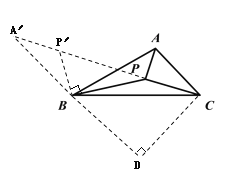
由题意,得![]()
∵A′B=AB=3,∠A′BA=90°,∠ABC=30°
∴∠A′BC=120°
∴∠CBD=60°
∵BC=4
∴BD=2,CD=![]()
∴A′C=![]() =
=![]()
故其最小值为![]() .
.

练习册系列答案
相关题目