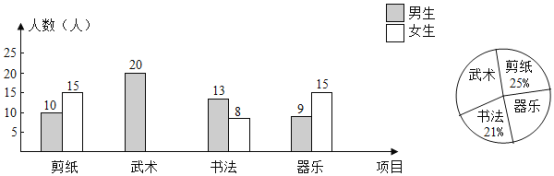
题目内容
【题目】已知:直线l:y=2kx-4k+3(k≠0)恒过某一定点P.
(1)求该定点P的坐标;
(2)已知点A、B坐标分别为(0,1)、(2,1),若直线l与线段AB相交,求k的取值范围;
(3)在0≤x≤2范围内,任取3个自变量x1,x2、x3,它们对应的函数值分别为y1、y2、y3,若以y1、y2、y3为长度的3条线段能围成三角形,求k的取值范围.
【答案】(1)(2,3);(2)k≥![]() ;(3)-
;(3)-![]() <k<0或0<k<
<k<0或0<k<![]() .
.
【解析】
(1)对题目中的函数解析式进行变形即可求得点P的坐标;
(2)根据题意可以得到相应的不等式组,从而可以求得k的取值范围;
(3)根据题意和三角形三边的关系,利用分类讨论的数学思想可以求得k的取值范围.
(1)∵y=2kx-4k+3=2k(x-2)+3,
∴y=2kx-4k+3(k≠0)恒过某一定点P的坐标为(2,3),
即点P的坐标为(2,3);
(2)∵点A、B坐标分别为(0,1)、(2,1),直线l与线段AB相交,直线l:y=2kx-4k+3(k≠0)恒过某一定点P(2,3),
∴![]() ,
,
解得,k≥![]() .
.
(3)当k>0时,直线y=2kx-4k+3中,y随x的增大而增大,
∴当0≤x≤2时,-4k+3≤y≤3,
∵以y1、y2、y3为长度的3条线段能围成三角形,
∴![]() ,
,
得k<![]() ,
,
∴0<k<![]() ;
;
当k<0时,直线y=2kx-4k+3中,y随x的增大而减小,
∴当0≤x≤2时,3≤y≤-4k+3,
∵以y1、y2、y3为长度的3条线段能围成三角形,
∴3+3>-4k+3,得k>-![]() ,
,
∴-![]() <k<0,
<k<0,
由上可得,-![]() <k<0或0<k<
<k<0或0<k<![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目