题目内容
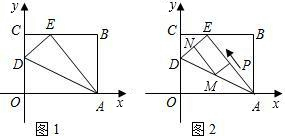
 OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.
OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.(1)如图,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作B′点.求B′点的坐标;
(2)求折痕CM所在直线的解析式.
分析:(1)折叠的性质得到CB′=CB=10,B′M=BM,在Rt△OCB′中,利用勾股定理易得OB′=8,即可得到B′点的坐标;
(2)设AM=t,则BM=B′M=6-t,而AB′=OA-OB′=2,在Rt△AB′M中,利用勾股定理求出t的值,确定M点的坐标,然后利用待定系数法求直线CM的解析式即可.
(2)设AM=t,则BM=B′M=6-t,而AB′=OA-OB′=2,在Rt△AB′M中,利用勾股定理求出t的值,确定M点的坐标,然后利用待定系数法求直线CM的解析式即可.
解答:解:(1)∵四边形ABCD为矩形,
∴CB=OA=10,AB=OC=6,
∵△CBM沿CM翻折后,点B落在x轴上,记作B′点,
∴CB′=CB=10,B′M=BM,
在Rt△OCB′中,OC=6,CB′=10,
∴OB′=8,
∴B′点的坐标为(8,0);
(2)设AM=t,则BM=B′M=6-t,
而AB′=OA-OB′=2,
在Rt△AB′M中,B′M2=B′A2+AM2,即(6-t)2=22+t2,解得t=
,
∴M点的坐标为(10,
),
设直线CM的解析式为y=kx+b,
把C(0,6)和M(10,
)代入得,b=6,10k+b=
,解得k=-
,b=6,
∴直线CM的解析式为y=-
x+6.
∴CB=OA=10,AB=OC=6,
∵△CBM沿CM翻折后,点B落在x轴上,记作B′点,
∴CB′=CB=10,B′M=BM,
在Rt△OCB′中,OC=6,CB′=10,
∴OB′=8,
∴B′点的坐标为(8,0);
(2)设AM=t,则BM=B′M=6-t,
而AB′=OA-OB′=2,
在Rt△AB′M中,B′M2=B′A2+AM2,即(6-t)2=22+t2,解得t=
| 8 |
| 3 |
∴M点的坐标为(10,
| 8 |
| 3 |
设直线CM的解析式为y=kx+b,
把C(0,6)和M(10,
| 8 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
∴直线CM的解析式为y=-
| 1 |
| 3 |
点评:本题考查了利用待定系数法求直线的解析式的方法:先设直线的解析式为y=kx+b,然后把已知两点的坐标代入求出k,b即可.也考查了折叠的性质以及勾股定理.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
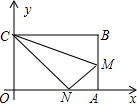 如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作N点.
如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作N点. 的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由. 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是