Question

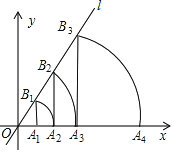
【题目】如图，已知的三个顶点、、，作关于直线的对称图形.

（1）若，试求四边形面积的最大值；

（2）若点恰好落在轴上，试求的值.

Answer 1

【答案】（1）9；（2）

【解析】

(1)如图1,易证,从而可得,根据二次函数的最值性就可解决问题

(2)如图2,易证,根据相似三角形的性质可得,然后在中运用勾股定理就可解决问题

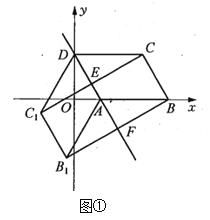
解析 （1）如图①，因为与四边形关于直线对称，

所以四边形是平行四边形，于点，于点，

则，，，

所以四边形、、是矩形，

则，

所以.

因为、、，

所以，，

所以，

则.由于，

所以当时，的最大值为9.

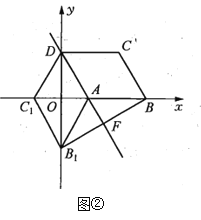
（2）当点恰好落在轴上时，如图②所示.因为于点，于点，所以，，

所以，又，

所以，

所以，

即，

解得.

由轴对称的性质可得.

在中，由勾股定理得，

整理得.

因为，

所以，

则得.