题目内容
【题目】如图,在 Rt△ABC 中,∠A=90°,∠C=30°.将△ABC 绕点 B 顺时针旋转 60°得到△A'BC',其中点 A',C'分别是点 A,C 的对应点.
(1)作出△A'BC'(要求尺规作图,不写作法,保留作图痕迹);
(2)连接 AA',求∠C'A'A 的度数.
【答案】(1)见解析(2)150°
【解析】
(1)直接利用等边三角形的性质得出对应点位置进而得出答案;
(2)直接利用等边三角形的判定方法△ABA′为等边三角形,得出进而得出答案.
(1)如图所示:△A'BC'即为所求;
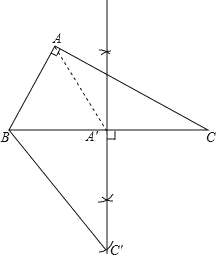
(2)在 Rt△ABC 中,∵∠C=30°,∠A=90°,
∴∠B=60°,
∵△A′B′C′由△ABC 旋转所得,
∴△A′B′C′≌△ABC,
∴BA=BA′,∠BA′C′=∠BAC=90°,
∴△ABA′为等腰三角形,
又∵∠ABC=60°,
∴△ABA′为等边三角形,
∴∠BA′A=60°,
∴ ∠C′A′A=∠BA′C′+∠BA′A=150°.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目