题目内容
【题目】分析探索题：细心观察如图，认真分析各式，然后解答问题．
OA22=（
）2+1=2 S1=
；
OA32=（
）2+1=3 S2=
；
OA42=（
）2+1=4 S3=
…
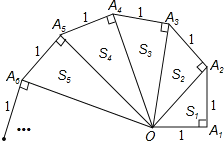
（1）请用含有n（n为正整数）的等式Sn= ；
（2）推算出OA10= ．
（3）求出 S12+S22+S32+…+S102的值．
【答案】（1）
；（2）
；（3）S12+S22+S32+…+S102=
．
【解析】
试题分析：（1）此题要利用直角三角形的面积公式，观察上述结论，会发现，第n个图形的一直角边就是
，然后利用面积公式可得．
（2）由同述OA2=
，0A3=
…可知OA10=
．
（3）S12+S22+S32+…+S102的值就是把面积的平方相加就可．
解：（1）
+1=n+1
Sn=
（n是正整数）；
故答案是：；
（2）∵OA12=1，
OA22=（
）2+1=2，
OA32=（
）2+1=3，
OA42=（
）2+1=4，
∴OA12=，
OA2=，
OA3=，…
∴OA10=
；
故答案是：；
（3）S12+S22+S32+…+S102
=（
）2+（
）2+（
）2+…+（
）2
=
（1+2+3+…+10）
=．
即：S12+S22+S32+…+S102=．
练习册系列答案
相关题目
【题目】某景点的门票价格如表：
购票人数/人 | 1～50 | 51～100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级（1）、（2）两班计划去游览该景点，其中（1）班人数少于50人，（2）班人数多于50人且少于100人，如果两班都以班为单位单独购票，则一共支付1118元；如果两班联合起来作为一个团体购票，则只需花费816元．
（1）两个班各有多少名学生？
（2）团体购票与单独购票相比较，两个班各节约了多少钱？