题目内容
【题目】如图,在半径为2的⊙O中,弦AB长为2.

(1)求点O到AB的距离.
(2)若点C为⊙O上一点(不与点A,B重合),求∠BCA的度数.
【答案】(1)点O到AB的距离为![]() ;(2)∠BCA的度数为30°或150°.
;(2)∠BCA的度数为30°或150°.
【解析】
试题分析:(1)过点O作OC⊥AB于点C,证出△OAB是等边三角形,继而求得∠AOB的度数,然后由三角函数的性质,求得点O到AB的距离;
(2)证出△ABO是等边三角形得出∠AOB=60°. 再分两种情况:点C在优弧![]() 上,则∠BCA=30°;点C在劣弧
上,则∠BCA=30°;点C在劣弧![]() 上,则∠BCA=
上,则∠BCA=![]() (360°﹣∠AOB)=150°;即可得出结果.
(360°﹣∠AOB)=150°;即可得出结果.
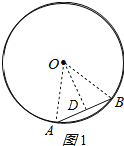
解:(1)过点O作OD⊥AB于点D,连接AO,BO.如图1所示:
∵OD⊥AB且过圆心,AB=2,
∴AD=![]() AB=1,∠ADO=90°,
AB=1,∠ADO=90°,
在Rt△ADO中,∠ADO=90°,AO=2,AD=1,
∴OD=![]() =
=![]() .
.
即点O到AB的距离为![]() .
.
(2)如图2所示:
∵AO=BO=2,AB=2,
∴△ABO是等边三角形,
∴∠AOB=60°.
若点C在优弧![]() 上,则∠BCA=30°;
上,则∠BCA=30°;
若点C在劣弧![]() 上,则∠BCA=
上,则∠BCA=![]() (360°﹣∠AOB)=150°;
(360°﹣∠AOB)=150°;
综上所述:∠BCA的度数为30°或150°.
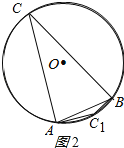

练习册系列答案
相关题目