题目内容
【题目】如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E，试找出图中的一个等腰三角形（△ABC除外），并说明理由．我找的等腰三角形是 理由：
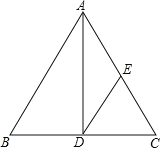
【答案】△EDC与△AED．
【解析】
试题分析：由AD是等腰三角形ABC的底边BC上的高，DE∥AB，易得△EDC是等腰三角形，又由AD⊥BC，易得△AED是等腰三角形．
解：△EDC与△AED．
理由：∵△ABC是等腰三角形，AB=AC，
∴∠B=∠C，
∵DE∥AB，
∴∠EDC=∠B，
∴∠EDC=∠C，
∴ED=EC，
即△EDC是等腰三角形；
∵AD⊥BC，
∴∠EDC+∠ADE=90°，∠C+∠CAD=90°，
∴∠ADE=∠CAD，
∴AE=ED，
∴△AED是等腰三角形．
故答案为：△EDC与△AED．
练习册系列答案
相关题目
