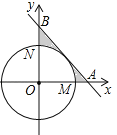题目内容
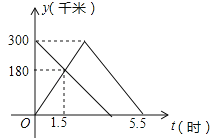
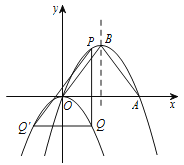
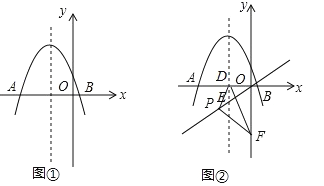
【题目】如图,在平面直角坐标系中,抛物线![]() (m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线
(m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线![]() 相交于点E,与x轴相交于点D,点P在直线
相交于点E,与x轴相交于点D,点P在直线![]() 上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
(1)如图①所示,若抛物线顶点的纵坐标为![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)求A、B两点的坐标;
(3)如图②所示,小红在探究点P的位置发现:当点P与点E重合时,∠PDF的大小为定值,进而猜想:对于直线![]() 上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
【答案】(1)![]() ;(2)A(﹣5,0)、B(1,0);(3)∠PDF=60°.
;(2)A(﹣5,0)、B(1,0);(3)∠PDF=60°.
【解析】
试题分析:(1)先提取公式因式将原式变形为![]() ,然后令y=0可求得函数图象与x轴的交点坐标,从而可求得点A、B的坐标,然后依据抛物线的对称性可得到抛物线的对称轴为x=﹣2,故此可知当x=﹣2时,y=
,然后令y=0可求得函数图象与x轴的交点坐标,从而可求得点A、B的坐标,然后依据抛物线的对称性可得到抛物线的对称轴为x=﹣2,故此可知当x=﹣2时,y=![]() ,于是可求得m的值;
,于是可求得m的值;
(2)由(1)的可知点A、B的坐标;
(3)先由一次函数的解析式得到∠PBF的度数,然后再由PD⊥PF,FO⊥OD,证明点O、D、P、F共圆,最后依据圆周角定理可证明∠PDF=60°.
试题解析:(1)∵![]() ,∴
,∴![]() =m(x+5)(x﹣1).令y=0得:m(x+5)(x﹣1)=0,∵m≠0,∴x=﹣5或x=1,∴A(﹣5,0)、B(1,0),∴抛物线的对称轴为x=﹣2.∵抛物线的顶点坐标为为
=m(x+5)(x﹣1).令y=0得:m(x+5)(x﹣1)=0,∵m≠0,∴x=﹣5或x=1,∴A(﹣5,0)、B(1,0),∴抛物线的对称轴为x=﹣2.∵抛物线的顶点坐标为为![]() ,∴﹣9m=
,∴﹣9m=![]() ,∴m=
,∴m=![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ;
;
(2)由(1)可知:A(﹣5,0)、B(1,0);
(3)∠PDF=60°.理由如下:
如图所示,∵OP的解析式为![]() ,∴∠AOP=30°,∴∠PBF=60°
,∴∠AOP=30°,∴∠PBF=60°
∵PD⊥PF,FO⊥OD,∴∠DPF=∠FOD=90°,∴∠DPF+∠FOD=180°,∴点O、D、P、F共圆,∴∠PDF=∠PBF,∴∠PDF=60°.

 名校课堂系列答案
名校课堂系列答案