题目内容
将抛物线 向左平移2个单位后所得到的抛物线为( )
向左平移2个单位后所得到的抛物线为( )
A. | B. | C. | D. |
D.
解析试题分析:根据二次函数图象的平移规律:左右平移,x改变:左加右减,y不变;上下平移,x不变,y改变,上加下减进行计算即可.
故选D.
考点:二次函数表达式.

练习册系列答案
相关题目
如图,二次函数y=ax2+bx+c的图象经过点(0,﹣2),与x轴交点的横坐标分别为x1,x2,且﹣1<x1<0,1<x2<2,下列结论正确的是( )
| A.a<0 | B.a﹣b+c<0 |
C. >1 >1 | D.4ac﹣b2<﹣8a |
抛物线 与y轴的交点坐标是( )
与y轴的交点坐标是( )
| A.(4,0) | B.(-4,0) | C.(0,-4) | D.(0,4) |
若直线 在第二、四象限都无图像,则抛物线
在第二、四象限都无图像,则抛物线 ( )
( )
| A.开口向上,对称轴是y轴 | B.开口向下,对称轴平行于y轴 |
| C.开口向上,对称轴平行于y轴 | D.开口向下,对称轴是y轴 |
二次函数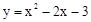 ,当y<0时,自变量x的取值范围是( )
,当y<0时,自变量x的取值范围是( )
A. 1<x<3 1<x<3 | B.x< 1 1 | C.x>3 | D.x< 1或x>3 1或x>3 |
将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( )
| A.y=x2+1 | B.y=x2﹣1 | C.y=(x﹣1)2 | D.y=(x+1)2 |
已知二次函数 的图象如图所示,有下列5个结论:①
的图象如图所示,有下列5个结论:① ;②
;②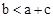 ;③
;③ ;④
;④ ;⑤
;⑤ ,(
,( 的实数)其中正确的结论有( )
的实数)其中正确的结论有( )
| A.2个 | B.3个 | C.4个 | D.5个 |
在平面直角坐标系中,将抛物线 绕着原点旋转180°,所得抛物线的解析式是( ).
绕着原点旋转180°,所得抛物线的解析式是( ).
| A.y=-(x-1)2-2 | B.y=-(x+1)2-2 |
C. | D. |
若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(﹣2,0),则抛物线y=ax2+bx的对称轴为【 】
| A.直线x=1 | B.直线x=﹣2 | C.直线x=﹣1 | D.直线x=﹣4 |