题目内容
如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD= 度.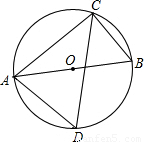
【答案】分析:先根据圆周角定理求出∠ACB及∠BCD的度数,再由∠ACD=∠ACB-∠BCD即可得出结论.
解答:解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD=50°,
∴∠ACD=∠ACB-∠BCD=90°-50°=40°.
故答案为:40.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
解答:解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD=50°,
∴∠ACD=∠ACB-∠BCD=90°-50°=40°.
故答案为:40.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 如图,△ABC的三个顶点都在同一个圆上,∠BAC的平分线AE交BC于点D,交这个圆于点E.求证:BE2=ED•EA.
如图,△ABC的三个顶点都在同一个圆上,∠BAC的平分线AE交BC于点D,交这个圆于点E.求证:BE2=ED•EA. 如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD=
如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD=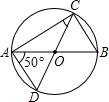 如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD的度数是
如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD的度数是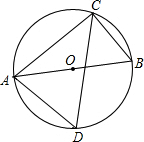 如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD=________度.
如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD=________度.