题目内容
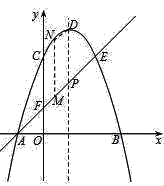
【题目】在平面直角坐标系xOy中，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，顶点为D，过点A的直线与抛物线交于点E，与y轴交于点F，且点B的坐标为（3，0），点E的坐标为（2，3）．
（1）求抛物线的解析式；
（2）若点G为抛物线对称轴上的一个动点，H为x轴上一点，当以点C、G、H、F四点所围成的四边形的周长最小时，求出这个最小值及点G、H的坐标；
（3）设直线AE与抛物线对称轴的交点为P，M为直线AE上的任意一点，过点M作MN∥PD交抛物线于点N，以P、D、M、N为顶点的四边形能否为平行四边形？若能，请求点M的坐标；若不能，请说明理由．
【答案】（1）抛物线的解析式为：y=﹣x2+2x+3；（2）G（1，1），H（
，0），四边形CFHG的周长最小值2+2
；（3）M的坐标为：M（0，1）或（
，
）或（
，
）．
【解析】
(1)根据抛物线上的两点列方程组求抛物线y=﹣x2+bx+c中的系数b和c，(2)根据题目的提示可以画出简图，然后表示出以点C、G、H、F四点所围成的四边形的周长，在根据表示出的线段就可以求出最短的周长，对应的点G、H的坐标也可得出；（3）根据题意可以分两种情况讨论，点N在点M的上方或者下方，然后设出点M，根据题目给出的条件是否能将P、D、M、N为顶点的四边形组成平行四边形，可以根据平行四边形对边相等来入手.
（1）∵y=﹣x2+bx+c经过（3，0）和（2，3），
∴
，
解得：
，
∴抛物线的解析式为：y=﹣x2+2x+3；
（2）∵y=﹣x2+2x+3，
∴y=﹣（x﹣1）2+4，
∴对称轴为x=1．
当y=0时，﹣x2+2x+3=0，
∴x1=﹣1，x2=3，
∴A（﹣1，0）．
当x=0时，y=3，
∴C（0，3）
∴CE=2．OC=3
如图，在y轴的负半轴上取一点I，使得点F点I关于x轴对称，在x轴上取点H，连接HF、HI、HG、GC、GE、则HF=HI．
∵抛物线的对称轴为x=1，
∴点C点E关于对称轴x=1对称，
∴CG=EG．
设直线AE的解析式为y=kx+b，由题意，得
，
解得：
，
∴直线AE的解析式为y=x+1．
当x=0时，y=1，
∴F（0，1），
∴OF=1，CF=2．
∵点F与点I关于x轴对称，
∴I（0，﹣1），
∴OI=1，CI=4．
在Rt△CIE中，由勾股定理，得
EI=
=2
．
∵要使四边形CFHG的周长最小，而CF是定值，
∴只要使CG+GH+HF最小即可．
∵CG+GH+HF=EG+GH+HI，
∴只有当EI为一条直线时，EG+GH+HI最小．
设EI的解析式为y=k1x+b1，由题意，得
，
解得：
，
∴直线EI的解析式为：y=2x﹣1，
∵当x=1时，y=1，
∴G（1，1）．
∵当y=0时，x
，
∴H（，0），
∴四边形CFHG的周长最小值=CF+CG+GH=CF+EI=2+2
；
（3）∵y=﹣x2+2x+3，
∴y=﹣（x﹣1）2+4，
∴D（1，4）
∴直线AE的解析式为y=x+1．
∴x=1时，y=2，
∴P（1，2），
∴PD=2．
∵四边形DPMN是平行四边形，
∴PD=MN=2．
∵点M在AE上，设M（x，x+1），
①当点M在线段AE上时，点N点M的上方，则N（x，x+3），
∵N点在抛物线上，
∴x+3=﹣x2+2x+3，
解得：x=0或x=1（舍去）
∴M（0，1）．
②当点M在线段AE或EA的延长线上时，点N在M的下方，则N（x，x﹣1）．
∵N点在抛物线上，
∴x﹣1=﹣x2+2x+3，
解得：x=
或x=
，
∴M（，
）或（，
）．
∴M的坐标为：M（0，1）或（
，
）或（
，）．
