题目内容
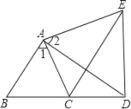
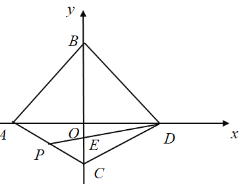
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 在
在![]() 轴负半轴上,且
轴负半轴上,且![]() ,把
,把![]() 沿
沿![]() 轴翻折,使点
轴翻折,使点![]() 落在
落在![]() 轴上的点
轴上的点![]() 处,点
处,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,则直线
,则直线![]() 的解析式为__________.
的解析式为__________.
【答案】![]()
【解析】
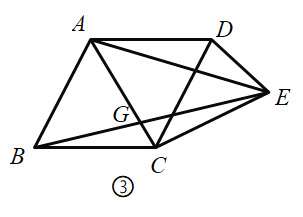
先求出点A、B坐标,于是可得OC的长,然后在Rt△AOC中根据三角函数的定义即可求出∠ACB=60°,延长AC到Q,使CQ=CB,连接BP,过D作DK∥y轴交CQ于K,如图,根据SAS可证△CBD≌△CQD,从而得∠CBD=∠Q,BD=DQ,根据等量代换和等腰三角形的性质可得∠DPQ=∠CBD,然后根据三角形的内角和定理可得∠BDP=∠ACB=60°,由此可得△PBD是等边三角形,进一步即可推得△DCK也是等边三角形,于是有DK=CK=CD=6m,根据SAS可证△BDC≌△PDK,从而得PK=BC=9m,再根据平行线分线段成比例定理即可列方程求出m的值,进一步即可求得D点坐标,然后根据待定系数法即可求出结果.
解:在![]() 中,
中,
令y=0,则![]() ,解得:x=﹣3
,解得:x=﹣3![]() m,令x=0,则y=6m,
m,令x=0,则y=6m,
∴点A(﹣3![]() m,0),B(0,6m),
m,0),B(0,6m),
∴AO=3![]() m,OB=6m,
m,OB=6m,
∵OB=2OC,∴OC=![]() OB=3m,
OB=3m,
在Rt△AOC中,∵tan∠ACB=![]() ,
,
∴∠ACB=60°,∴∠OAC=30°,
如图,延长AC到Q,使CQ=CB,连接BP,过D作DK∥y轴交CQ于K,
∵∠ACB=∠BCD=60°,∴∠DCQ=60°,
∴∠BCD=∠DCQ,
∵CD=CD,
∴△CBD≌△CQD(SAS),
∴∠CBD=∠Q,BD=DQ,
∵BD=PD,∴PD=DQ,
∴∠DPQ=∠Q,
∴∠DPQ=∠DBC,
∵∠CEP=∠DEB,
∴∠PCB=∠BDP=60°,

∵BD=PD,∴△PBD为等边三角形,
∵DK∥y轴,∴∠DKC=∠ACB=60°,
∵∠DCK=60°,∴△DCK是等边三角形,
∴DK=CK=CD=6m,
∵∠BDP=∠CDK=60°,
∴∠BDC=∠PDK,
∵BD=PD,CD=DK,
∴△BDC≌△PDK(SAS),
∴PK=BC=9m,∴PC=3m,
∵点E的纵坐标为﹣1,∴OE=1,
∴CE=3m﹣1,
∵CE∥DK,∴![]() ,
,
∴![]() ,解得:m=1,
,解得:m=1,
∴D(3![]() ,0),E(0,﹣1),
,0),E(0,﹣1),
设直线PD的解析式为y=kx+b,
∴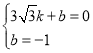 ,解得:
,解得: ,
,
∴直线PD的解析式为![]() .
.