题目内容
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字-1、-2、0;先从甲袋中随机取出一个小球,记录标有的数字为x,再从乙袋中随机取出一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
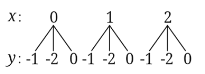
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x2-1的图象上的概率;
(3)若以点M为圆心,2为半径作⊙M,求⊙M与坐标轴相切的概率.
【答案】(1)答案见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1) 根据题意画出树状图即可.
(2)分别将各点坐标代入函数y=-x2-1解析式, 若等式成立, 则该点在其图象上, 用满足条件的M点的个数除以M点总个数即为所求概率。
(3) 分别计算各点到0点的距离, 若OM> 2, 则在⊙0上或⊙0外, 可以过M点作⊙0的切线,满足条件的M点的个数除以M点总个数即为所求概率.
解:(1) 树状图如图所示, 则M所有可能的坐标有9种情况,分别为:(0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1),(2,-2),(2,0).
(2) 将 (1) 中的9个坐标分别代入函数y=-x2-1, 可得在函数的图象上的M点有两个: (0,-1), (1,-2),所以点M在函数y=-x2+1的图象上的概率为![]() .
.
(3) 要过M作圆的切线, 则该点应该在圆上或者圆外, 通过比较OM与半径长度可知, 点M在⊙0上或⊙0外的有5个, 分别为(0,-2),(1,-2),(2,-1),(2,-2),(2,0).则过M点能作⊙0的切线的概率为![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目