题目内容
【题目】《九章算术》中“今有勾七步，股有二十四步，问勾中容圆径几何？”其意思是：“今有直角三角形，勾(短直角边)长为7步，股(长直角边)长为24步，问该直角三角形的容圆(内切圆)直径是多少？”( )
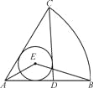
A. 4步 B. 5步 C. 6步 D. 8步
【答案】C
【解析】
设三角形△ABC，由勾股定理可求得直角三角形的斜边，设内切圆的半径为r，由S△ABC=
（AB+BC+CA）r可求得半径，则可求得直径．
解：设三角形为△ABC，∠C=90°，AC=7，BC=24，
∴AB=
=
=25，
设内切圆的半径为r，则S△ABC=（AB+BC+CA）r，
∴ACBC=（AB+BC+CA）r，即×7×24=×（7+24+25）r，
解得r=3，
∴内切圆的直径是6步，
故选：C．
练习册系列答案
相关题目
