题目内容
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
(1)如图①,当点H与点C重合时,可得FGFD.(大小关系)
(2)如图②,当点H为边CD上任意一点时,猜想FG与FD的数量关系,并说明理由.
(3)在图②中,当AB=8,BE=3时,利用探究的结论,求CF的长.
【答案】
(1)=
(2)
解:猜想FD=FG.
证明:连接AF,
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
![]() ,
,
∴△AGF≌△ADF.
∴FG=FD
(3)
解:设FG=x,
∵AB=8,BE=3,
∴BC=CD=8,
∴FC=8﹣x,FE=3+x,EC=8﹣3=5,
在Rt△ECF中,EF2=FC2+EC2,即(3+x)2=(8﹣x)2+52,
解得x= ![]() .
.
∴CF=8﹣ ![]() =
= ![]() ,
,
即FG的长为 ![]()
【解析】解:(1)连接AF,
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,![]() ,
,
∴△AGF≌△ADF.
∴FG=FD.
故答案为:=;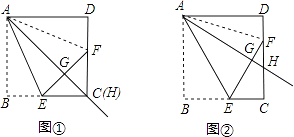
(1)连接AF,根据图形猜想FD=FG,由折叠的性质可得AB=AG=AD,再结合AF为△AGF和△ADF的公共边,从而证明△AGF≌△ADF,从而得出结论.(2)连接AF,根据图形猜想FD=FG,由折叠的性质可得AB=AG=AD,再结合AF为△AGF和△ADF的公共边,从而证明△AGF≌△ADF,从而得出结论.(3)设FG=x,则FC=8﹣x,FE=3+x,在Rt△ECF中利用勾股定理可求出x的值,进而可得出答案.

练习册系列答案
相关题目