Question

【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D ， 如果AC=3，AB=6，那么AD的值为（　　）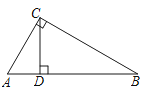
A.
B.
C.
D.

Answer 1

【答案】A
【解析】解答：如图，∵在Rt△ABC中，∠ACB=90°，CD⊥AB ，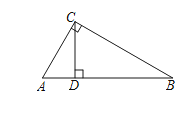
∴AC2=ADAB ，
又∵AC=3，AB=6，
∴32=6AD ， 则AD=
故选：A
分析：先证明△BAD∽△BCA ， 则利用相似的性质得AB：BC=BD：AB ， 然后根据比例性质得到AB2=BCBD.
【考点精析】掌握解直角三角形是解答本题的根本，需要知道解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．