题目内容
【题目】综合题。
(1)解方程:x2﹣4x﹣3=0
(2)解不等式组: 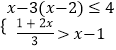 并将解集在数轴上表示出来.
并将解集在数轴上表示出来.
【答案】
(1)解:∵△=(﹣4)2﹣4×1×(﹣3)=28>0,
∴x= ![]() =2
=2 ![]() ,
,
故方程的解为:x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ;
;
(2)解:解不等式x﹣3(x﹣2)≤4,得:x≥1,
解不等式 ![]() ,得:x<4,
,得:x<4,
故不等式组的解集为:1≤x<4.
解集在数轴上表示为:

【解析】(1)公式法求解可得;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【考点精析】关于本题考查的一元一次不等式组的解法,需要了解解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能得出正确答案.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目