题目内容
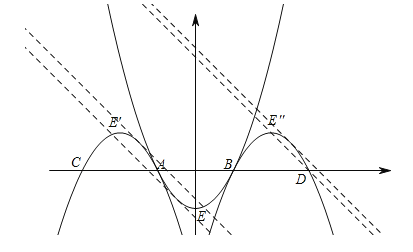
【题目】抛物线C1:y=x2﹣1(﹣1≤x≤1)与x轴交于A、B两点,抛物线C2与抛物线C1关于点A中心对称,抛物线C3与抛物线C1关于点B中心对称.若直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点,则b的取值或取值范围是_____.
【答案】b=-![]() 或-
或-![]() 或3
或3![]()
【解析】分析:根据对称性先求抛物线C2与抛物线C3的解析式,再分两种情况:
①在y轴右侧时,从直线y=﹣x+b与C3相切时到直线过点D时,这些b值符合条件,计算出来即可;
②在y轴的左侧,当y=﹣x+b与C1相切时和y=﹣x+b与C2相切时,都与C2有C1、C2、C3组成的图形恰好有2个公共点,分别计算出b的值.
详解:抛物线C1:y=x2﹣1(﹣1≤x≤1),顶点E(0,﹣1),当y=0时,x=±1,∴A(﹣1,0),B(1,0),当抛物线C2与抛物线C1关于点A中心对称,∴顶点E关于点A的对称点E′(﹣2,1),∴抛物线C2的解析式为:y=﹣(x+2)2+1=﹣x2﹣4x﹣3,当抛物线C3与抛物线C1关于点B中心对称,∴顶点E关于点B的对称点E′′(2,1),∴抛物线C3的解析式为:y=﹣(x﹣2)2+1=﹣x2+4x﹣3.分两种情况讨论:
①当y=﹣x+b过D(3,0)时,b=3,当y=﹣x+b与C3相切时,即与C3有一个公共点,则![]() ,﹣x2+4x﹣3=﹣x+b,x2﹣5x+b+3=0,△=25﹣4(b+3)=0,b=
,﹣x2+4x﹣3=﹣x+b,x2﹣5x+b+3=0,△=25﹣4(b+3)=0,b=![]() ,∴当3≤b<
,∴当3≤b<![]() 时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点;
时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点;
②当y=﹣x+b与C1相切时,即与C1有一个公共点,则![]() ,x2﹣1=﹣x+b,x2+x﹣1﹣b=0,△=1﹣4(﹣1﹣b)=0,b=﹣
,x2﹣1=﹣x+b,x2+x﹣1﹣b=0,△=1﹣4(﹣1﹣b)=0,b=﹣![]() ,当y=﹣x+b与C2相切时,即与C2有一个公共点,则
,当y=﹣x+b与C2相切时,即与C2有一个公共点,则![]() ,﹣x2﹣4x﹣3=﹣x+b,﹣x2﹣3x﹣3﹣b=0,△=9﹣4×(﹣1)×(﹣3﹣b)=0,b=﹣
,﹣x2﹣4x﹣3=﹣x+b,﹣x2﹣3x﹣3﹣b=0,△=9﹣4×(﹣1)×(﹣3﹣b)=0,b=﹣![]() ,∴当b=﹣
,∴当b=﹣![]() 或﹣
或﹣![]() 时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点.
时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点.
综上所述:当b=﹣![]() 或﹣
或﹣![]() 或3≤b<
或3≤b<![]() 时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点.
时,直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点.