题目内容
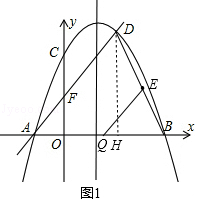
【题目】已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).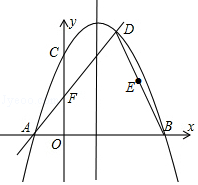
(1)求二次函数的解析式并写出D点坐标;
(2)点E是BD的中点,点Q是线段AB上一动点,当△QBE和△ABD相似时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.
【答案】
(1)
解:(1)由题可得: 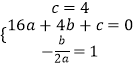 ,
,
解得: 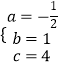 ,
,
则二次函数的解析式为y=﹣ ![]() x2+x+4.
x2+x+4.
∵点D(2,m)在抛物线上,
∴m=﹣ ![]() ×22+2+4=4,
×22+2+4=4,
(2)
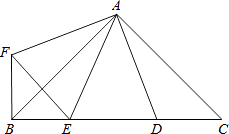
解:过点D作DH⊥AB于点H,如图1,
∵点D(2,4),点B(4,0),
∴DH=4,OH=2,OB=4,
∴BH=2,∴DB= ![]() =2
=2 ![]() .
.
∵点E为DB的中点,
∴BE= ![]() BD=
BD= ![]() .
.
令y=0,得﹣ ![]() x2+x+4=0,
x2+x+4=0,
解得:x1=4,x2=﹣2,
∴点A为(﹣2,0),
∴AB=4﹣(﹣2)=6.
①若△QBE∽△ABD,
则 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:BQ=3,
∴OQ=OB﹣BQ=4﹣3=1,
∴点Q的坐标为(1,0);
②若△QBE∽△DBA,
则 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BQ= ![]() ,
,
∴OQ=OB﹣BQ=4﹣ ![]() =
= ![]() ,
,
∴点Q的坐标为( ![]() ,0).
,0).
综上所述:点Q的坐标为(1,0)或( ![]() ,0);
,0);
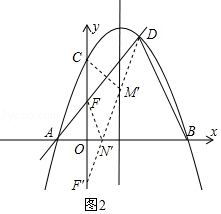
(3)
解:如图2,由A(﹣2,0),D(2,4),
可求得直线AD的解析式为:y=x+2,
即点F的坐标为:F(0,2),
过点F作关于x轴的对称点F′,即F′(0,﹣2),连接DF′交对称轴于M′,x轴于N′,
由条件可知,点C,D是关于对称轴x=1对称,
则CF+F′N+M′N′+M′C=CF+DF′=2+2 ![]() ,
,
则四边形CFNM的周长=CF+FN+NM+MC≥CF+FN′+M′N′+M′C,
即四边形CFNM的最短周长为:2+2 ![]() .
.
此时直线DF′的解析式为:y=3x﹣2,
所以存在点N的坐标为N( ![]() ,0),点M的坐标为M(1,1).
,0),点M的坐标为M(1,1).
【解析】(1)首先运用待定系数法求出二次函数的解析式,然后把点D(2,m)代入二次函数的解析式,就可求出点D的坐标;(2)过点D作DH⊥AB于点H,如图1,根据勾股定理可求出BD,易求出点A的坐标,从而得到AB长,然后分两种情况:①△QBE∽△ABD,②△QBE∽△DBA讨论,运用相似三角形的性质求出BQ,从而得到OQ,即可得到点Q的坐标;(3)根据待定系数法得到直线AD的解析式为:y=x+2,过点F作关于x轴的对称点F′,即F′(0,﹣2),连接DF′交对称轴于M′,x轴于N′,由条件可知,点C,D是关于对称轴x=1对称,则CF+F′N+M′N′+M′C=CF+DF′=2+2 ![]() ,得到四边形CFNM的最短周长为:2+2
,得到四边形CFNM的最短周长为:2+2 ![]() 时直线DF′的解析式为:y=3x﹣2,从而得到满足条件的点M和点N的坐标.
时直线DF′的解析式为:y=3x﹣2,从而得到满足条件的点M和点N的坐标.
【考点精析】本题主要考查了勾股定理的概念和相似三角形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.

【题目】某公司欲招收职员一名,从学历、经验和工作态度等三个方面对甲乙丙进行了初步测试,测试成绩如下表.
(1)如果将学历、经验和工作态度三项得分按![]() 的比例确定各人的最终得分,并以此为据确定录用者,那么谁将被录用?
的比例确定各人的最终得分,并以此为据确定录用者,那么谁将被录用?
(2)自己确定学历、经验和工作态度三项的权,并根据自己的方案确定录用者.
应聘者 | 甲 | 乙 | 丙 |
项目 | |||
学历 |
|
|
|
经验 |
|
|
|
工作态度 |
|
|
|
【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁): 39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
总 计 | 50 |
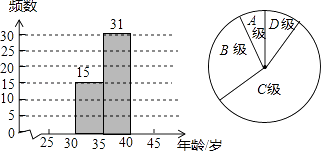
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.