题目内容
根据条件求值:①设a=2-
 ,求a2+
,求a2+ -2的值.
-2的值.②设a2+b2-4a-2b+5=0,求
 的值.
的值.③已知:
 +
+ =
=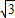 +
+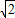 ,
,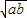 =
=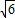 -
-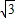 ,求a+b的值.
,求a+b的值.④已知
 -
- =2,求
=2,求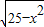 +
+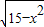 的值.
的值.
【答案】分析:①中,显然运用完全平方公式,再代入计算;
②中,首先由配方法确定a和b的值,再代入计算;
③中,注意运用完全平方公式解决.a+b=( +
+ )2-2
)2-2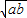 ;
;
④中,注意运用平方差公式.
解答:解:①∵a=2- ,∴a2+
,∴a2+ -2=(a-
-2=(a-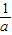 )2=(2-
)2=(2-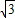 -
- )2=(2-
)2=(2-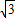 -2-
-2- )2=12;
)2=12;
②∵a2+b2-4a-2b+5=0,
∴(a-2)2+(b-1)2=0
∴a=2,b=1,
∴原式= =
= ;
;
③∵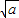 +
+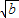 =
=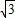 +
+ ,
, =
= -
- ,
,
∴a+b=( +
+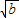 )2-2
)2-2 =(
=(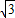 +
+ )2-2
)2-2 +2
+2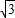 =5+2
=5+2 ;
;
④∵( +
+ )(
)( -
- )=25-x2-15+x2=10,
)=25-x2-15+x2=10,
又知 -
-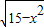 =2,
=2,
∴ +
+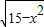 =10÷2=5.
=10÷2=5.
点评:此题中,要求对完全平方公式和平方差公式的变形非常熟悉.同时注意二次根式的一些性质:当a≥0时,a=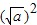 .
.
②中,首先由配方法确定a和b的值,再代入计算;
③中,注意运用完全平方公式解决.a+b=(
 +
+ )2-2
)2-2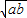 ;
;④中,注意运用平方差公式.
解答:解:①∵a=2-
 ,∴a2+
,∴a2+ -2=(a-
-2=(a-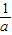 )2=(2-
)2=(2-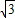 -
- )2=(2-
)2=(2-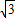 -2-
-2- )2=12;
)2=12;②∵a2+b2-4a-2b+5=0,
∴(a-2)2+(b-1)2=0
∴a=2,b=1,
∴原式=
 =
= ;
;③∵
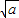 +
+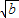 =
=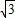 +
+ ,
, =
= -
- ,
,∴a+b=(
 +
+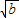 )2-2
)2-2 =(
=(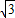 +
+ )2-2
)2-2 +2
+2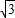 =5+2
=5+2 ;
;④∵(
 +
+ )(
)( -
- )=25-x2-15+x2=10,
)=25-x2-15+x2=10,又知
 -
-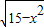 =2,
=2,∴
 +
+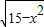 =10÷2=5.
=10÷2=5.点评:此题中,要求对完全平方公式和平方差公式的变形非常熟悉.同时注意二次根式的一些性质:当a≥0时,a=
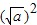 .
. 
练习册系列答案
相关题目
 ,求a2+
,求a2+ -2的值.
-2的值.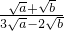 的值.
的值.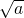 +
+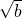 =
= ,
,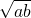 =
= -
-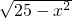 -
-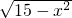 =2,求
=2,求