题目内容
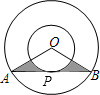 如图,两个同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6、3,则图中阴影部分的面积为
如图,两个同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6、3,则图中阴影部分的面积为分析:连接OP,根据切线的性质和两个圆的半径,可求得∠A的度数,由勾股定理得出AP的长,进而得出∠AOB,用△AOB的面积减去扇形OCD的面积.
解答: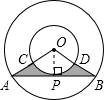 解:如图,∵AB切大⊙O,
解:如图,∵AB切大⊙O,
∴∠APO=90°,
∵OA=6,OP=3,
∴∠A=30°,AP=3
,
∴∠AOB=120°,
∴S阴影=S△AOB-S扇形OCD=
-
=9
-3π.
故答案为:9
-3π.
 解:如图,∵AB切大⊙O,
解:如图,∵AB切大⊙O,∴∠APO=90°,
∵OA=6,OP=3,
∴∠A=30°,AP=3
| 3 |
∴∠AOB=120°,
∴S阴影=S△AOB-S扇形OCD=
3
| ||
| 2 |
| 120•π•32 |
| 360 |
| 3 |
故答案为:9
| 3 |
点评:本题考查了切线的性质和扇形面积的计算,以及等腰三角形的性质,是基础题,难度不大.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
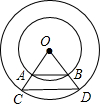 如图,两个同心圆的圆心为O,大圆的半径OC、OD交小圆于A、B,试探究AB与CD有怎样的位置关系?
如图,两个同心圆的圆心为O,大圆的半径OC、OD交小圆于A、B,试探究AB与CD有怎样的位置关系?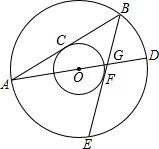 弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.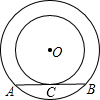 如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB=( )
如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB=( ) (2009•莱芜)如图,两个同心圆的圆心为O,EC是大圆的一条弦,交小圆于D、B两点,已知弦心距OA=3,DB=8,EC=l2,则圆环(阴影部分)的面积为( )
(2009•莱芜)如图,两个同心圆的圆心为O,EC是大圆的一条弦,交小圆于D、B两点,已知弦心距OA=3,DB=8,EC=l2,则圆环(阴影部分)的面积为( )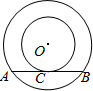 如图,两个同心圆的半径分别为6cm和10cm,弦AB与小圆相切于点C,则AB=
如图,两个同心圆的半径分别为6cm和10cm,弦AB与小圆相切于点C,则AB=