题目内容
【题目】定义: 数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹); 
(2)如图2,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= ![]() CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用:
CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用: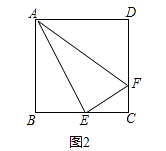
(3)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时点P的坐标. 
【答案】
(1)解:如图1所示

(2)解:△AEF是否为“智慧三角形”,
理由如下:设正方形的边长为4a,
∵E是DC的中点,
∴DE=CE=2a,
∵BC:FC=4:1,
∴FC=a,BF=4a﹣a=3a,
在Rt△ADE中,AE2=(4a)2+(2a)2=20a2,
在Rt△ECF中,EF2=(2a)2+a2=5a2,
在Rt△ABF中,AF2=(4a)2+(3a)2=25a2,
∴AE2+EF2=AF2,
∴△AEF是直角三角形,
∵斜边AF上的中线等于AF的一半,
∴△AEF为“智慧三角形”;
(3)解:如图3所示:

由“智慧三角形”的定义可得△OPQ为直角三角形,
根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,
由垂线段最短可得斜边最短为3,
由勾股定理可得PQ= ![]() =2
=2 ![]() ,
,
PM=1×2 ![]() ÷3=
÷3= ![]() ,
,
由勾股定理可求得OM= ![]() =
= ![]() ,
,
故点P的坐标(﹣ ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() ).
).
【解析】(1)连结AO并且延长交圆于C1 , 连结BO并且延长交圆于C2 , 即可求解;(2)设正方形的边长为4a,表示出DF=CF以及EC、BE的长,然后根据勾股定理列式表示出AF2、EF2、AE2 , 再根据勾股定理逆定理判定△AEF是直角三角形,由直角三角形的性质可得△AEF为“智慧三角形”;(3)根据“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,根据勾股定理可求另一条直角边,再根据三角形面积可求斜边的高,即点P的横坐标,再根据勾股定理可求点P的纵坐标,从而求解.

【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
“文明在我身边”摄影比赛成绩统计表
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x≤100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题:
(1)统计表中c的值为;样本成绩的中位数落在分数段中;
(2)补全频数分布直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?