题目内容
 将两个全等的直角三角形ABC和DBE按图1方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
将两个全等的直角三角形ABC和DBE按图1方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;
(2)若将图1中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其他条件不变,请在图2中画出变换后的图形,并直接写出(1)中的结论是否仍然成立.
分析:(1)连接BF,证△BCF≌△BEF,推出CF=EF,即DE=AC=AF+CF=AF+EF;
(2)连接BF,证△BCF≌△BEF,推出CF=EF,即DE=AC=AF+CF=AF+EF.
(2)连接BF,证△BCF≌△BEF,推出CF=EF,即DE=AC=AF+CF=AF+EF.
解答:(1)证明:连接BF,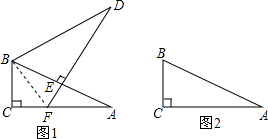
∵△ABC≌△DBE,
∴BC=BE,
∵∠C=∠AEF=90°,
∴在△BCF和△BEF中
∴△BCF≌△BEF,
∴CF=EF,
∴AF+EF=AC=DE.
(2)AF+EF=DE,
同(1)得CF=EF,
∵△ABC≌△DBE,
∴AC=DE,
∴AF+FC=AF+EF=AC=DE.

∵△ABC≌△DBE,
∴BC=BE,
∵∠C=∠AEF=90°,
∴在△BCF和△BEF中
|
∴△BCF≌△BEF,
∴CF=EF,
∴AF+EF=AC=DE.
(2)AF+EF=DE,

同(1)得CF=EF,
∵△ABC≌△DBE,
∴AC=DE,
∴AF+FC=AF+EF=AC=DE.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的性质是:①全等三角形的对应边相等,对应角相等,②全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目