题目内容
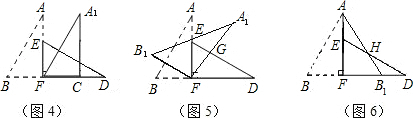
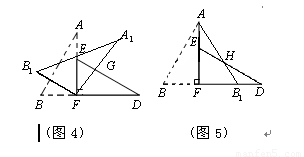
如图1,小明将一张矩形纸片沿对角线剪开,得到两张全等直角三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、F、D在同一条直线上,F为公共直角顶点.
小明在对这两张三角形纸片进行如下操作时遇到了两个问题,请你帮助解决.
(1)将图3中的△ABF绕点F顺时针方向旋转30°到图4的位置,A1F交DE于点G,请你求出线段FG的长度;
(2)将图3中的△ABF沿直线AF翻折到图5的位置,AB1交DE于点H,请证明:AH=DH.
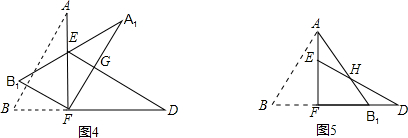
分析:(1)在Rt△EFD中,求出FD的长,根据直角三角形的性质,可得:FG=
FD,即可求得FG的值;
(2)借助平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,容易证明.
| 1 |
| 2 |
(2)借助平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,容易证明.
解答:解:(1)∵∠A1FA=30°,
∴∠GFD=60°,∠D=30°,
∴∠FGD=90°,
在Rt△EFD中,ED=10cm,
∵FD=5
,
∴FG=
cm;
(2)△AHE与△DHB1中,
∵∠FAB1=∠EDF=30°,
∴FD=FA,EF=FB=FB1,
∴FD-FB1=FA-FE,即AE=DB1,
又∵∠AHE=∠DHB1,
∴△AHE≌△DHB1(AAS),
∴AH=DH.
∴∠GFD=60°,∠D=30°,
∴∠FGD=90°,
在Rt△EFD中,ED=10cm,
∵FD=5
| 3 |
∴FG=
5
| ||
| 2 |
(2)△AHE与△DHB1中,
∵∠FAB1=∠EDF=30°,
∴FD=FA,EF=FB=FB1,
∴FD-FB1=FA-FE,即AE=DB1,
又∵∠AHE=∠DHB1,
∴△AHE≌△DHB1(AAS),
∴AH=DH.
点评:本题是一道全等三角形的判定、旋转的性质、平移的性质和直角三角形的性质结合求解的综合题.考查学生综合运用数学的能力.

练习册系列答案
相关题目